Question
Question: Two points A and B are located in diametrically opposite directions of a point charge of \(+2\mu C\)...
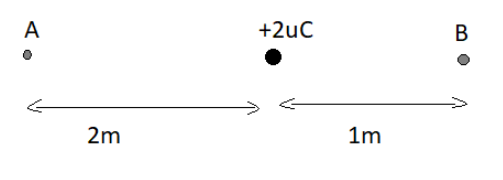
Two points A and B are located in diametrically opposite directions of a point charge of +2μC at distances 2 m and 1 m respectively from it. The potential difference between A and B is
A. 3×103V
B. 6×104V
C. −9×103V
D. −3×103V
Solution
To solve this problem we will calculate the potential at point A and B due to a point charge of+2μCcharge and take a difference for the required answer. We will also discuss some factors and points regarding potential due to point charges and potential due to multiple charges in the system.
Formula used:
Potential due to point charge Is given by,
⇒V=4π∈∘1rq
Complete Step by step solution:
Electric potential at some point in the electric field is defined as the amount of work done on a unit positive charge in moving from infinity to that point along any path under the electrostatic force exerted on it.
The electric potential at any point at distance r from a charged particle is given as,
⇒V=4π∈∘1rq, here q(charge on a source object ), r(position vector of point charge ) and ∈∘(constant)
Unit of potential is Volt, and 1 volt
⇒V=coulombjoule=JC−1
Now, potential difference between A and B due to point charge of +2μC will be given as,
⇒V=4π∈∘q[rA1−rb1]
rA(distance of A from point charge) and rB(distance of B from point charge )
⇒V=2×10−6×9×109[21−11]
⇒V=−9×103V
∴The potential difference between point A and B due to point charge particle of +2μCis ,
⇒V=−9×103V, hence option (C) is correct.
Note:
In the above problem we have discussed potential due to a point charge but if we have multiple charges q1,q2,q3....qn exerting potential at a point from distance r1,r2,r3....rn, we can get the electrostatic potential at a point by calculating potential from each charges one by one and by adding them algebraically to calculate total potential at that point, the mathematical expression for the same is given below,
⇒V=4π∈∘1i=1∑nriqi
