Question

Two point-masses m and 4 m are separated by a distance d on a line. A third point mass ${m_0}$is to be placed at a point on the line such that the net gravitational force on it is zero. The distance of that point from the m mass is

Answer 1

For the gravitational force to be zero on the line joining these two masses, there must be equal and opposite forces acting on the mass at a point on the line. By equating the forces, we can find the distance at which this occurs.

Complete step by step solution:
The concept of gravitational force is based on the Newton’s law of universal gravitation which states that – everybody in this universe exerts a gravitational force on another body whose magnitude is directly proportional to the product of the masses of the bodies and inversely proportional to the square of distance between the bodies and acts along the line joining the centres of the two bodies.
If two bodies of mass ${m_1}$ and ${m_2}$ are separated by a distance r,
Gravitational force,
$F \propto {m_1}{m_2}$
$F \propto \dfrac{1}{{{r^2}}}$
Combining,
$F \propto \dfrac{{{m_1}{m_2}}}{{{r^2}}}$
$\Rightarrow F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}$
where G is called the universal gravitational constant and its value is equal to $6 \cdot 67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$
Consider two point-masses of mass m and 4m separated by a distance d. Let a point mass ${m_0}$ be kept at a distance of $x$ from the mass m, such that the net gravitational force acting on it is zero, as shown:

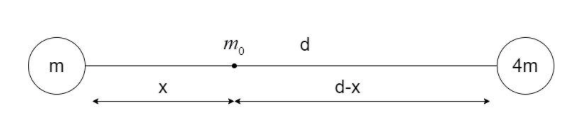
The gravitational force experienced by ${m_0}$ from both the masses is equal.
Hence,
${F_1} = {F_2}$
$\dfrac{{G \times m \times {m_0}}}{{{x^2}}} = \dfrac{{G \times 4m \times {m_0}}}{{{{\left( {d - x} \right)}^2}}}$
$\Rightarrow \dfrac{{{{\left( {d - x} \right)}^2}}}{{{x^2}}} = 4$
$\Rightarrow \dfrac{{{{\left( {d - x} \right)}^2}}}{{{x^2}}} = {2^2}$
Squaring on both sides
$\dfrac{{d - x}}{x} = 2$
$\Rightarrow d - x = 2x$
$\Rightarrow 3x = d$
$\therefore x = \dfrac{d}{3}$
The distance at which the mass should be placed is 1/3rd of the total distance of separation, measured from the mass m.

Note: The principle that says that the equal forces acting on the opposite directions cause net effect to be zero, is the principle of equilibrium of forces. According to the equilibrium of forces, Net forces in the direction X = 0 $\sum {F_x} = 0$