Question

Two-point masses having mass $M$ and $4M$ are placed at a distance $r$. The gravitational potential at a point, where gravitational field intensity zero is-
(A) $\dfrac{{ - 9GM}}{r}$
(B) $\dfrac{{ - 2GM}}{{3r}}$
(C) $\dfrac{{ - 3GM}}{r}$
(D) $\dfrac{{ - 6GM}}{{5r}}$

Answer 1

As we all know that the gravitational field is zero where the force of gravitation applied by both the bodies on a unit mass placed in between the line of action of the force of two bodies is equal and hence the net force at a point becomes zero.

Complete answer:
Consider the gravitational field at a point $P$ is equal to zero which is located at a distance $x$ from mass $M$ . Assume that a unit mass is located at a point $P$.

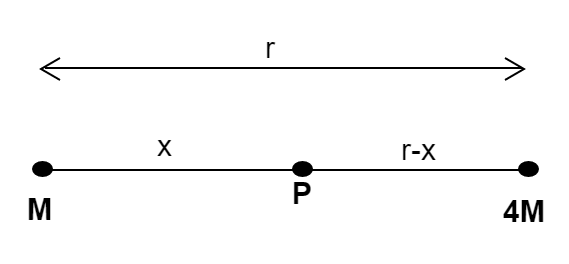
As we all know that subsequently, the gravitational field at a point $P$ is zero, so it can be said that the gravitational pull exerted by the body of mass $M$ on a unit mass at $P$ i.e. ${F_1}$ is equal to the gravitational pull exerted by the body of mass $4M$ on a unit mass i.e. ${F_2}$.
Therefore, we can say that the relationship becomes,
${F_1} = {F_2}$
$\Rightarrow \dfrac{{GM}}{{{x^2}}} = \dfrac{{G\left( {4M} \right)}}{{{{\left( {r - x} \right)}^2}}}$
Taking $\;GM$ both the sides common and cancelling out we get,
$\dfrac{{{{\left( {r - x} \right)}^2}}}{{{x^2}}} = 4$
$\Rightarrow \dfrac{{\left( {r - x} \right)}}{x} = 2$
On further solving the above equation we get,
$x = \dfrac{r}{3}$
Now we will find the Gravitational potential at the point $P$. So the gravitational potential ${V_P}$ at point $P$ is,
${V_P} = \dfrac{{ - GM}}{x} - \dfrac{{G\left( {4M} \right)}}{{r - x}}$ .............. $\left( 1 \right)$
We will substitute $x = \dfrac{r}{3}$ in the equation $\left( 1 \right)$ and the result would become;
${V_P} = - \dfrac{{GM}}{{\dfrac{r}{3}}} - \dfrac{{4GM}}{{r - \dfrac{r}{3}}}$
$\Rightarrow {V_P} = - \dfrac{{GM}}{{\dfrac{r}{3}}} - \dfrac{{4GM}}{{\dfrac{{2r}}{3}}}$
On further solving the above equation we get,
${V_P} = \dfrac{{ - 2GM - 4GM}}{{\dfrac{{2r}}{3}}}$
$\Rightarrow {V_P} = - \dfrac{{9GM}}{r}$
At the point where the gravitational field is zero, the gravitational potential is equal to $- \dfrac{{9GM}}{r}$ .

Therefore, the correct answer to this question is (A) $- \dfrac{{9GM}}{r}$ .

Note:
As we all know, the work done per unit mass that is required to move an object from another location to some reference fixed point, is called Gravitational potential. It is analogous to electric potential and here the mass plays the role of the charge.