Question
Question: Two point electric charges of values q and 2q are kept at a distance d apart from each other in air....
Two point electric charges of values q and 2q are kept at a distance d apart from each other in air. A third charge Q is to be kept along the same line in such a way that the net force acting on q and 2q is zero. Find the location of the third charge from charge q.
(a). 1+2d
(b). 1−2d
(c). 1+6d
(d). 1−6d
Solution
Hint: Net force on the charge q and 2q should be zero according to the question. So, charge Q should be negative and should be placed in between the charges q and 2q. Then Coulomb’s law can be used to determine the forces on charge q and 2q due to other charges. Then we can compare the equations given to determine the distance of charge Q from the charge q.
Formulae used:
Electrostatic force between two charges Q1 and Q2 placed at a distance r using the formula, F=r2kQ1Q2, where k is the electrostatic constant.
Complete step-by-step answer:
We have been given that the two charges q and 2q are placed at a distance d from each other. And a third charge Q has been placed along their line of joining, such that net force on charges q and 2q is zero.
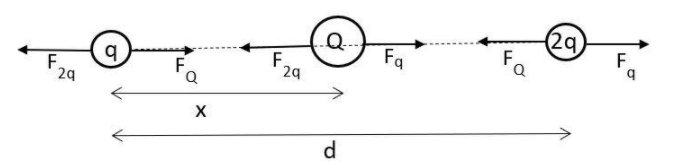
For the given conditions to prevail, the charge Q should be negative and should be placed in between the charges q and 2q. Assume charge Q is placed at a distance x from the charge q.
Using Coulomb’s law, we can express the electrostatic force of attraction or repulsion between two charges Q1 and Q2 placed at a distance r using the formula, F=r2kQ1Q2, where k is the electrostatic constant.
Now, force acting on charge q due to charge Q should be balanced by the force due to the charge 2q.
Therefore, FQ=F2q
⟹x2kqQ=d22kq2 ………. (i)
Similarly, forces acting on charge 2q due to charges Q and q should balance each other
Therefore, Fq=FQ
⟹d22kq2=(d−x)22kQq ………. (ii)
Now, from equation (i) and (ii), we can write,
x2kqQ=(d−x)22kQq
⟹x21=(d−x)22
⟹(xd−x)2=2
⟹x=2+1d
Hence, option a is the correct answer.
Note: One should be careful while placing the charge Q. If we assume the charge to be negative and place it on the line joining the charges q and 2q either on the left of q or in between q and 2q or in the right of 2q, there will only be the repulsion forces, that will disbalance the forces. So we need to consider charge Q as negative.
