Question

Two point charges $q_A = 5\mu C$ and $q_B = -5\mu C$ are located at A and B separated by $0.2\;m$ in vacuum.
A. What is the electric field at the midpoint O of the line joining the charges?
B. If a negative test charge of magnitude $2\;nC$ is placed at O, what is the force experienced by the test charge?

Answer 1

For the first part, the electric field at point O will arise due to the electric field at this point due to the presence of charges A and B. In such a case, the net electric field at O will be the sum of electric fields at O due to A and that due to B. For the second part, the test charge is subject to the same electric field at point O. Using the fact that the force acting on the test charge will be proportional to the electric field at O and the magnitude of the test charge, obtain the numerical value for the force as experienced by the test charge.

Formula used: Electric field strength $E =\dfrac{1}{4\pi\epsilon_0}\dfrac{|q|}{r^2}$
Force acting on a charge in an electric field: $F = Eq$

Complete step by step answer:
The magnitude of electric field due to a charge q at a distance r from the charge is given as:
$|E|=\dfrac{1}{4\pi\epsilon_0}\dfrac{|q|}{r^2}$.
Now, we know that electric field lines are always directed away from positive charges and towards negative chargesLet the electric field at O due to the A be $E_{OA}$ and let the electric field at O due to B be $E_{OB}$. The distance between $q_A$ and O will be equal to distance between $q_B$ and O since O is the midpoint, and will have a value $r = \dfrac{0.2}{2} = 0.1\;m$
A. Let the electric field at the mid-point between the two charges be $E_O$. This will be the additive sum of the electric field due to charges A and B at O.

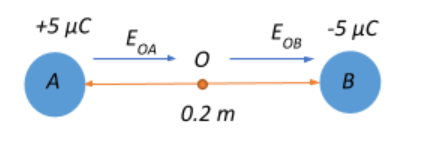
$\Rightarrow E_O = E_{OA}+E_{OB}$
Now, $E_{OA} = \dfrac{1}{4\pi\epsilon_0}.\dfrac{5 \times 10^{-6}}{0.1^2}$
Similarly, $E_{OB} = \dfrac{1}{4\pi\epsilon_0}.\dfrac{5 \times 10^{-6}}{0.1^2}$
Therefore, $E_O = \dfrac{1}{4\pi\epsilon_0}.\dfrac{5 \times 10^{-6}}{0.1^2} +\dfrac{1}{4\pi\epsilon_0}.\dfrac{5 \times 10^{-6}}{0.1^2} = 2 \times \dfrac{1}{4\pi\epsilon_0}.\dfrac{5 \times 10^{-6}}{10^{-2}}$
$\Rightarrow E_O = 2(9 \times 10^9)(5 \times 10^{-4}) = 90 \times 10^5\;Vm^{-1}$
B. We are given that a test charge of $2\;nC$ is placed at O. The test charge experiences the same electric field $E_O$ since the strength of the electric field depends on the source charges and is independent of the test charge.

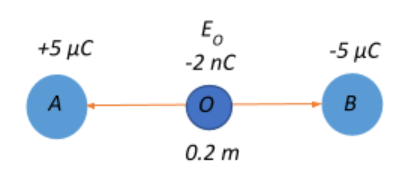
Therefore, the force experienced by the test charge $q = 2 \times 10^{-9}C$ can be given as:
$F = E_0 \times q = (90 \times 10^{5}) \times (2 \times 10^{-9}) = 180 \times 10^{-4}\;N$

Note: Always remember that the effective electric field experienced by any charge q at a point will depend only on the source charge producing the field and is in no way influenced by the magnitude of the test charge placed at that point. However, the force experienced by the test charge as a consequence of its presence in the electric field will depend on the magnitude of the test charge.
Do not forget that if the electric field has a + sign, it means that the field is directed away from the charge, and if it has a – sign, it means that the field is directed towards the charge. Thus, the sign indicates the direction of the electric field. However, we have only considered the magnitudes and their effective contributions in the above problem since only that is of relevance to us.