Question

Two point charges $+8\;q$ and $-2\;q$ are located at $x=0$ and $x=L$ respectively. The location of a point on the $x$ -axis at which the net electric field due to these two point charges is zero:
(A) $2\;L$
(B) $\dfrac{L}{4}$
(C) $8\;L$
(D) $4\;L$

Answer 1

Hint : To find the point at which the net electric field is zero, we need to consider the whole $x$ -axis and find where the electric field by the positive charge and negative charge oppose each other.

Complete Step By Step Answer:
Here, we are given two charges ${{q}_{1}}=+8q$ and ${{q}_{2}}=-2q$ that are separated by a distance $x=L$ .
Let us plot the arrangement of the charges on the $x$ -axis,

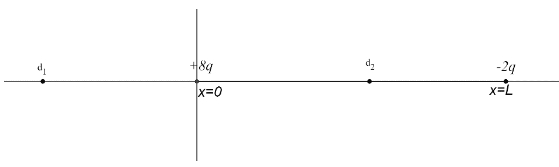
We know that the direction of the electric field for a positive charge is away from the charge and the direction of the electric field for a negative charge is towards the charge.
The electric field can be calculated by the formula,
$E=\dfrac{kq}{{{r}^{2}}}$
where, $k$ = Coulomb’s Constant = $9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}$
$q$ is the charge of the particle
$r$ is the distance of the point from the charge at which the electric field is to be found.
Now, to find the point where the net electric field is zero, we need to consider three different cases
For the range $-\infty Consider a point$ d_1 $in the region$ -\infty Hence, as the fields oppose each other, there might exist a point, where the net field is zero.
For the range $0Consider a point$ d_2 $in the region$ 0Hence, as the fields are in the same direction, at no point the electric field is possible to be zero.
For the range $LConsider a point$ d_3 $in the region$ LHence, as the fields oppose each other, there might exist a point, where the net field is zero.
Hence, the point for zero electric field cannot lie between the charges. Consider the point to be at a distance $d$ from the positive charge $+8q$
Now, from the formula of electric field, the total electric field for both charges is
$E=\dfrac{k(+8q)}{{{(d)}^{2}}}+\dfrac{k(-2q)}{{{(L+d)}^{2}}}$ for the range $-\infty$ E=\dfrac{k(+8q)}{{{(d)}^{2}}}+\dfrac{k(-2q)}{{{(d-L)}^{2}}} $for the range$ LHence, an equivalent equation is given as,
$E=\dfrac{k(+8q)}{{{(d)}^{2}}}+\dfrac{k(-2q)}{{{(d\pm L)}^{2}}}$
We need the electric field to be zero.
$\therefore 0=\dfrac{k(+8q)}{{{(d)}^{2}}}+\dfrac{k(-2q)}{{{(d\pm L)}^{2}}}$
$\therefore \dfrac{k(2q)}{{{(d\pm L)}^{2}}}=\dfrac{k(8q)}{{{(d)}^{2}}}$
Canceling the common terms,
$\therefore \dfrac{(2)}{{{(d\pm L)}^{2}}}=\dfrac{(8)}{{{(d)}^{2}}}$
Rearranging the equation,
$\therefore \dfrac{{{d}^{2}}}{{{(d\pm L)}^{2}}}=\dfrac{8}{2}$
$\therefore \dfrac{{{d}^{2}}}{{{(d\pm L)}^{2}}}=4$
Applying square root on both sides,
$\therefore \dfrac{d}{d\pm L}=2$
Now, we consider two cases,
$\therefore \dfrac{d}{d+L}=2$
Cross multiplying the denominator,
$\therefore d=2(d+L)$
$\therefore d=2d+2L$
Hence, the value of distance is,
$\therefore d=-2L$
$\therefore \dfrac{d}{d-L}=2$
Cross multiplying the denominator,
$\therefore d=2(d-L)$
$\therefore d=2d-2L$
Hence, the value of distance is,
$\therefore d=2L$
Hence, the correct answer is Option $(A)$ .

Note :
The note to remember here is that the electric field for a positive charge is always spreading outside, going away from the charge, while the electric field for a negative charge is always converging inside, coming towards the charge. Hence, we can understand for two different charges, the net electric field is zero at an external point. While, for two similar charges, the net electric field will be zero at a point between the charges.