Solveeit Logo
Login

Question

Question: Two point charges \(1\times 10^{-3}C\) and \(4\times 10^{-3}C\) are located \(0.0\;6m\) apart in air...

Two point charges 1×10−3C1\times 10^{-3}C and 4×10−3C4\times 10^{-3}C are located 0.0  6m0.0\;6m apart in air. Find the location of the point between them where the resultant electric field is zero.

Explanation

Solution

Electric field is the electric force due to a unit positive charge which is at rest would exert on its surrounding. We can find the electric field due to the individual charges and then equate them to each other, to find the point where they are equal.

Formula used: E=FqE=\dfrac{F}{q}orE=kqr2E=\dfrac{kq}{r^{2}}

Complete step by step answer:
We know that the electric force due to a pair of charges is given by Coulomb's law. An electric field can be produced by a time-varying electric field or an electrical charge. These can be either attracting or repelling in nature.
An electric field E is defined as the electric force F per unit positive charge q , which is infinitesimally small and at rest, and is given as E=FqE=\dfrac{F}{q}. ThenE=kqr2E=\dfrac{kq}{r^{2}}, where k=14πϵ0k=\dfrac{1}{4\pi\epsilon_{0}} which is a constant and rr is the distance between the unit charges.
Given that the charges are q1=1×10−3Cq_{1}=1\times 10^{-3}C and q2=4×10−3Cq_{2}=4\times 10^{-3}C, also given that they are at a distance r=0.0  6mr=0.0\;6m from each other. For the electric fields to cancel each other, another point charge qq must be placed at a distance xx from q1q_{1}

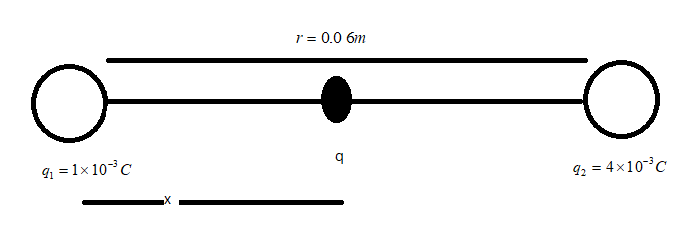
Then the electric field on qq is given as,
kq1x2=kq2(r−x)2\dfrac{kq_{1}}{x^{2}}=\dfrac{kq_{2}}{(r-x)^{2}}
  ⟹  (r−x)2x2=q2q1\implies \dfrac{(r-x)^{2}}{x^{2}}=\dfrac{q_{2}}{q_{1}}
  ⟹  r−xx=q1q2\implies \dfrac{r-x}{x}=\sqrt{\dfrac{q_{1}}{q_{2}}}
Substituting the values we get,
  ⟹  0.06−xx=1×10−34×10−3\implies\dfrac{0.06-x}{x}=\sqrt{\dfrac{1\times 10^{-3}}{4\times 10^{-3}}}
  ⟹  0.06−xx=14\implies\dfrac{0.06-x}{x}=\sqrt{\dfrac{1}{4}}
  ⟹  0.06−xx=12\implies\dfrac{0.06-x}{x}=\dfrac{1}{2}
  ⟹  0.12−2x=x\implies0.12-2x=x
  ⟹  0.12=3x\implies0.12=3x
  ⟹  x=0.04m\implies x=0.04m

Hence the distance at a distance 0.04  m0.04\;m from q1=10−3Cq_{1}=10^{-3}C the electric field cancels each other.

Note: Electric field is in the direction of the force. Usually, the electric field of a point positive charge is radially outwards, whereas the electric field of a point negative charge is radially inwards to the charge. However, the electric field also depends on the symmetry of the charge carrying conductor.