Question

Two plates (area=5) charged to $+ {q_1}$ and $+ {q_2}\left( {{q_2} < {q_1}} \right)$ are brought closer to form a capacitor of capacitance $C$ . The potential difference across the plates is:
(A) $\dfrac{{{q_1} - {q_2}}}{{2C}}$
(B) $\dfrac{{{q_1} - {q_2}}}{C}$
(C) $\dfrac{{{q_1} - {q_2}}}{{4C}}$
(D) $\dfrac{{2\left( {{q_1} - {q_2}} \right)}}{C}$

Answer 1

Find the electric field of the two plates using the formula and add both to find the net electric field. Substitute this value in the formula of the potential difference to find the relation of the voltage. Substitute the formula of the capacitance in it.

Formula used:
(1) The formula of the electric field is given by
$E = \dfrac{\sigma }{{2{ \in _0}}}$
Where $E$ is the electric field of the plate, $\sigma$ is the charge density of the plate and ${ \in _0}$ is the permittivity of the free space.
(2) The formula of the capacitance is given by
$C = \dfrac{{{ \in _0}A}}{d}$
Where $C$ is the capacitance of the plate, $A$ is its area and $d$ is the distance between the plates.
(3) The formula of the potential difference is given by
$V = Ed$
Where $V$ is the potential difference.

Complete answer:
It is given that the two plates has the area, $A = 5$
Charge of the plate one is greater than the charge of the plate two, ${q_2} < {q_1}$
The electric field of the first plate is ${E_1} = \dfrac{{{\sigma _1}}}{{2{ \in _0}}}$…………………..(1)
The electric field of the second plate is ${E_2} = \dfrac{{{\sigma _2}}}{{2{ \in _0}}}$ ……………….(2)

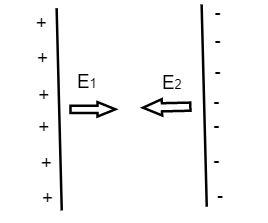
So the net electric field provided by the two plates as the capacitor is obtained by dividing the two electric fields offered by the individual plates.
${E_{net}} = {E_1} - {E_2}$
Substitute the equation (1) and (2) in the above equation, we get
${E_{net}} = \dfrac{{{\sigma _1}}}{{2{ \in _0}}} - \dfrac{{{\sigma _2}}}{{2{ \in _0}}}$
The charge density of the plate is given by dividing the charge per area of the plate. Substituting this in the above step, we get
${E_{net}} = \dfrac{1}{2}\dfrac{{\left( {{Q_1} - {Q_2}} \right)}}{{{ \in _0}A}}$-
Use the formula of the potential difference across the two plates,
$V = Ed$
Substitute the net electric field and the distance between the two plates in it,
$V = \dfrac{1}{2}\dfrac{{\left( {{Q_1} - {Q_2}} \right)}}{{{ \in _0}A}}d$
Substituting the formula of the capacitance in the above formula, we get
$V = \dfrac{1}{2}\dfrac{{\left( {{Q_1} - {Q_2}} \right)}}{C}$
Hence the potential difference across the two plates is given by $\dfrac{1}{2}\dfrac{{\left( {{Q_1} - {Q_2}} \right)}}{C}$ .

Thus the option (A) is correct.

Note:
When the two plates of the opposite charges are brought close to each other, then it behaves as the capacitor for storing the energy in the circuit. The energy is stored between the two plates by the electrostatic force and it does not dissipate energy. Remember the formula of the electric field and the capacitance to find the voltage drop across the plates.