Question

Two plano-concave lenses of glass of refractive index $1.5$ have radii of curvatures $20\ cm$, $30\ cm$. They are placed in contact with curved surfaces towards each other and space between them is filled with a liquid of refractive index $\dfrac{4}{3}$ . The focal length of the system is:
A. $48\ cm$
B. $72\ cm$
C. $12\ cm$
D. $24\ cm$

Answer 1

Hint: First of all we will draw the diagram as per the question and then consider any one side from where the rays are incidence. Then we will divide the lenses into two parts and we will find focal lengths of each lens using the formula, $\dfrac{1}{f}=\left( \mu -1 \right)\left[ \dfrac{1}{{{r}_{1}}}-\dfrac{1}{{{r}_{2}}} \right]$ and then we will find the overall focal length of the system using the formula of combination of lenses i.e $\dfrac{1}{{{f}_{eq}}}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}+\dfrac{1}{{{f}_{3}}}$.

Formula used: $\dfrac{1}{f}=\left( \mu -1 \right)\left[ \dfrac{1}{{{r}_{1}}}-\dfrac{1}{{{r}_{2}}} \right]$, $\dfrac{1}{{{f}_{eq}}}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}+\dfrac{1}{{{f}_{3}}}$

Complete step by step answer:
In question it is given that two plano-concave lenses of glass of refractive index $1.5$ have radii of curvatures $20\ cm$, $30\ cm$. They are placed in contact with curved surfaces towards each other and space between them is filled with a liquid of refractive index $\dfrac{4}{3}$. So, on the basis of it we will draw the figure,

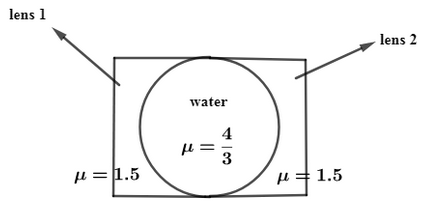
Now, as shown in the figure we will consider that rays are incidenced from the left side of the lens so first of all it will fall on lens 1, then pass through water and then it will fall on lens 2. First of all, we will consider the rays incidence on lens 1, so, the focal length can be given by the formula,
$\dfrac{1}{f}=\left( \mu -1 \right)\left[ \dfrac{1}{{{r}_{1}}}-\dfrac{1}{{{r}_{2}}} \right]$ …………………(i)
Where f is focal length, ${{r}_{1}}$ and ${{r}_{2}}$are radii of the lens, $\mu$ is the refractive index of the lens.
For lens 1, ${{r}_{1}}$ is infinite as it is plain mirror and ${{r}_{2}}$ will be $20\ cm$ and $\mu$ is given 1.5, now, substituting this values in equation we will get focal length of lens 1 as,
$\dfrac{1}{{{f}_{1}}}=\left( \mu -1 \right)\left[ \dfrac{1}{{{r}_{1}}}-\dfrac{1}{{{r}_{2}}} \right]$
$\dfrac{1}{{{f}_{1}}}=\left( 1.5-1 \right)\left[ \dfrac{1}{\infty }-\dfrac{1}{20} \right]\Rightarrow \dfrac{1}{{{f}_{1}}}=\left( 0.5 \right)\left[ -\dfrac{1}{20} \right]$
$\Rightarrow \dfrac{1}{{{f}_{1}}}=\left[ -\dfrac{0.5}{20} \right]\Rightarrow {{f}_{1}}=\left( -40 \right)\ cm$ ………….(ii)
In the same way, for lens 2 ${{r}_{2}}$is infinite as it is plain mirror and ${{r}_{1}}$ will be $30\ cm$ and $\mu$ is given 1.5, now, substituting this values in equation we will get focal length of lens 2 as,
$\dfrac{1}{{{f}_{2}}}=\left( \mu -1 \right)\left[ \dfrac{1}{{{r}_{1}}}-\dfrac{1}{{{r}_{2}}} \right]$
$\dfrac{1}{{{f}_{2}}}=\left( 1.5-1 \right)\left[ \dfrac{1}{30}-\dfrac{1}{\infty } \right]\Rightarrow \dfrac{1}{{{f}_{2}}}=\left( 0.5 \right)\left[ \dfrac{1}{30} \right]$
$\Rightarrow \dfrac{1}{{{f}_{2}}}=\left[ \dfrac{0.5}{30} \right]\Rightarrow {{f}_{2}}=\left( -60 \right)\ cm$ …………………..(iii)
As the lens is in the opposite direction to the direction of rays the focal length of lens 2 will be negative.
Now, for water, ${{r}_{1}}$ is $20\ cm$ mirror and ${{r}_{2}}$ will be $-30\ cm$ as the radii is in the opposite direction to the direction of incidence rays and $\mu$ is given $\dfrac{4}{3}$, now, substituting this values in equation we will get focal length of water as,
$\dfrac{1}{{{f}_{3}}}=\left( \mu -1 \right)\left[ \dfrac{1}{{{r}_{1}}}-\dfrac{1}{{{r}_{2}}} \right]$
$\dfrac{1}{{{f}_{3}}}=\left( \dfrac{4}{3}-1 \right)\left[ \dfrac{1}{20}-\dfrac{1}{-30} \right]\Rightarrow \dfrac{1}{{{f}_{3}}}=\left( \dfrac{1}{3} \right)\left[ \dfrac{1}{20}+\dfrac{1}{30} \right]$
$\Rightarrow \dfrac{1}{{{f}_{3}}}=\dfrac{1}{3}\left[ \dfrac{50}{600} \right]\Rightarrow {{f}_{3}}=\dfrac{600\times 3}{50}=36\ cm$
Now, we will use the formula of combination of lenses which is given as,
$\dfrac{1}{{{f}_{eq}}}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}+\dfrac{1}{{{f}_{3}}}$
Now, substituting the values from expression
$\Rightarrow \dfrac{1}{{{f}_{eq}}}=\dfrac{1}{-40}+\dfrac{1}{-60}+\dfrac{1}{36}$
$\Rightarrow \dfrac{1}{{{f}_{eq}}}=\dfrac{1}{-40}+\dfrac{1}{-60}+\dfrac{1}{36}\Rightarrow \dfrac{1}{{{f}_{eq}}}=\dfrac{\left( -60\times 36 \right)}{-40\times 60\times 36}+\dfrac{\left( -40\times 36 \right)}{-40\times -60\times 36}+\dfrac{\left( -40\times -60 \right)}{-40\times -60\times 36}$
$\Rightarrow \dfrac{1}{{{f}_{eq}}}=-\dfrac{1}{72}$
${{f}_{eq}}=-72\ cm$
Here, the value of focal length is negative which means the system will behave as a concave lens and overall focal length of the system is $-72\ cm$.

Note: Students might make mistakes in considering the direction of the rays and due to that they might make mistakes in considering the radius and focal length of the lens as positive or negative and due to that the whole sum will go wrong. So, students should take care while solving such problems.