Question

Two planes intersect to form a
(A) plane
(B) point
(C) straight line
(D) angle

Answer 1

Assume two planes $z=0$ and $y=0$ . The curve that is formed by the intersection of the planes whose equations are $z=0$ and $y=0$ will be common for both of the planes. Now, observe the curve, when these two planes intersect each other and conclude the answer.

Complete step by step answer:
According to the question, we are asked to find the curve when two planes intersect each other.
Let us proceed with a diagram.
Let us assume two planes $z=0$ and $y=0$ .
Here, the plane whose equation is $z=0$ is a vertical plane and the plane whose equation is $y=0$ is a horizontal plane.
We are asked to find the curve that is formed by the intersection of the planes whose equations are $z=0$ and $y=0$ .
The curve that is formed by the intersection of the planes whose equation are $z=0$ and $y=0$ will be common for both of the planes ……………………………………..(1)
Now, representing the planes $z=0$ and $y=0$ on the coordinate axes, we get

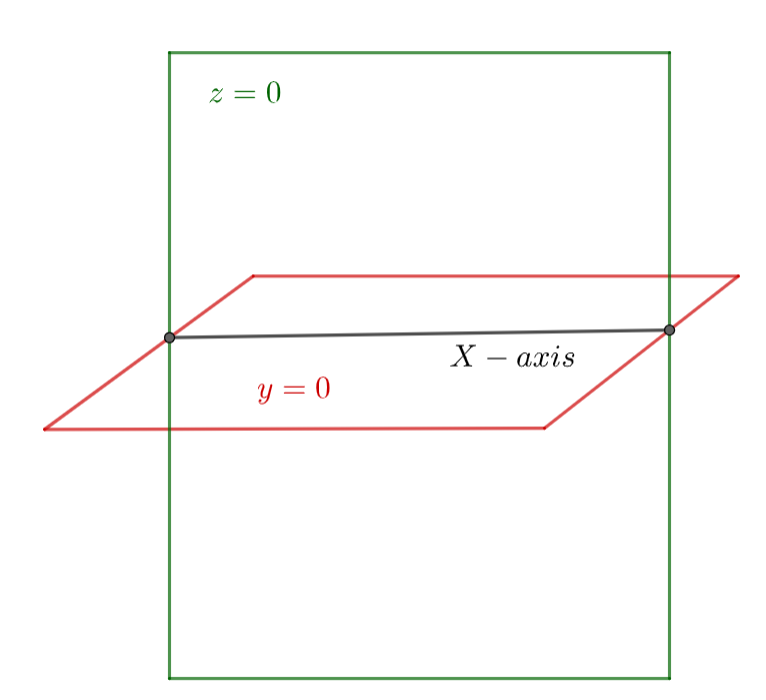
In the above figure, we can see that two planes are intersecting each other and there is a line that is common for both vertical and horizontal planes.
The line which is common for both planes is the x-axis …………………………………..(2)
Now, from equation (1) and equation (2), we can say that x-axis is the line of intersection of the planes $z=0$ and $y=0$ .
So, the x-axis is the line of intersection of planes $z=0$ and $y=0$ .

So, the correct answer is “Option C”.

Note: In this question, one might make a silly mistake and think that the intersection of two planes forms a plane. This is wrong. Therefore, always keep in mind that the intersection of two planes always forms a line. We must also know that the intersection of two lines results in a point.