Question

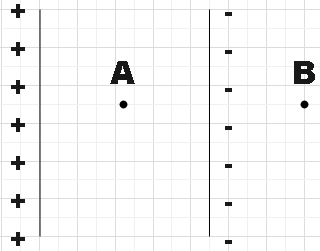
Two plane sheets of charge densities $+\sigma$ and $-\sigma$ are kept in air as shown. What are the electric field intensities (i) at a point A above both the plates and (ii) at a point B

Answer 1

You could first recall the electric field intensity due charged plane sheets. Then you may realize that the magnitude of charge density is the same for both sheets though they are of opposite charges. Now by taking care of the direction of the electric field intensities we could find the answer.
Formula used:
Electric field intensity due to charged plane sheet,
$E=\dfrac{\sigma }{2{{\varepsilon }_{0}}}$

Complete answer:
In the question we are given two plane sheets of opposite charge densities $+\sigma$ and$-\sigma$. We are supposed to find the electric field intensities at two marked points: point A in between the plane sheets and point B to the right of the negative plane sheet.
(i) Let us consider the point A in between the given plane sheets. The net electric field intensity in this region would be the sum of the electric field intensities due to both the given plane sheets but we have to take the direction of these fields into account. We know that the electric fields are directed from positive to negative. So, the electric field intensity on A due to the left plane sheet would be directed away from the plate and it would be directed towards the right plate with the same magnitude. (also the same direction)
Net electric field intensity at A would be,
${{E}_{A}}=\dfrac{\sigma }{2{{\varepsilon }_{0}}}+\dfrac{\sigma }{2{{\varepsilon }_{0}}}=\dfrac{2\sigma }{2{{\varepsilon }_{0}}}$
$\therefore {{E}_{A}}=\dfrac{\sigma }{{{\varepsilon }_{0}}}$
Hence, net electric field intensity at point A is found to be${{E}_{A}}=\dfrac{\sigma }{{{\varepsilon }_{0}}}$
(ii) Very similarly at point B, the electric field due to the left plate would be directed away from the plate and it would be directed towards the right plate (i.e, in opposite directions) with equal magnitudes.
Net electric field intensity at point B would be,
${{E}_{B}}=\dfrac{\sigma }{2{{\varepsilon }_{0}}}-\dfrac{\sigma }{2{{\varepsilon }_{0}}}$
$\therefore {{E}_{B}}=0$

Hence, net electric field intensity at point B is found to be zero.

Note:
We have solved this question from the known standard expression for electric field intensity due charged plane sheets. And now you know these standard expressions become handy in situations like this. We would have wasted a lot of time deriving that expression if we hadn’t known it already.