Question

Two plane mirrors ${M_1}$ and ${M_2}$ have a length of 1m each and are separated by 1 cm. A ray of light is incident on one end of a mirror ${M_1}$ at an angle of ${45^ \circ }$. How many reflections will the ray have before going out the other end?

(A) 50
(B) 51
(C) 100
(D) 101

Answer 1

Hint When light is reflected from a plane mirror, the incident angle and the reflected angle are the same. Calculate the distance covered by the light ray between two reflections and divide the total length of the plane mirrors by that distance to determine the number of reflections

Complete step by step answer
We know that:
Length of mirror is ${\text{L}} = 1m$
Distance between the mirrors is $d = 1\,cm\, = \,0.01\,m$
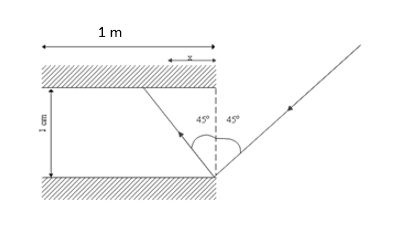
Since the light ray is incident on a plane mirror, the ray will be reflected at the same angle with respect to the normal at which it is incident, as shown below.

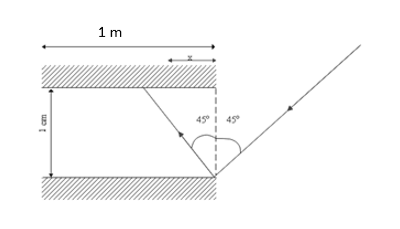
Suppose the ray covers a horizontal distance $x$ between two reflections. Further, let $n$ be the total number of reflections the light ray undergoes before it exits the system of two mirrors.
Since we want to find out the number of reflections before the light ray exits the system, it must cover a total horizontal distance $L$ in $n$ reflections. As the ray covers a distance $x$ between two reflections, to cover a distance $L$, we must have $nx = L$.
And we also know that
$\Rightarrow \tan \theta = \dfrac{x}{d} \\\ \Rightarrow x = d\tan \theta \\\$
On substituting the value of $x$ in $nx = L$, we get
$\Rightarrow n = \dfrac{L}{{d\tan \theta }}$
$\therefore n = \dfrac{1}{{0.01 \times \tan {{45}^o}}} = \dfrac{1}{{0.01 \times 1}} = 100$
But we have yet to count the first reflection that the light ray experiences when it enters the system. So, the total number of reflections that the light ray will experience $= 100 + 1 = 101$ which corresponds to option (D).
Hence, the correct option is option (D).

Note
We must not forget to count the first reflection separately which the light ray makes when it enters the system. Since the light ray covers a constant horizontal distance between two reflections, we don’t have to calculate the horizontal distance covered for each reflection individually. We must also make sure that the angle of reflection is measured with respect to the normal of the plane mirror.