Question

Two plane mirrors arranged at right angles to each other as shown in figure A. A ray of light is incident on the horizontal mirror at an angle $\theta$, for what value of $\theta$ the ray emerges parallel to the incoming ray after reflection from the vertical mirror.

(A) $60^\circ$
(B) $30^\circ$
(C) $45^\circ$
(D) All of these

Answer 1

Hint
For parallel emergent ray, the angle which the incident ray makes with the vertical (normal of horizontal mirror) must be equal to the angle of which the emergent ray (second reflected ray) makes with the vertical (surface of second mirror). Angle of reflection is equal to angle of incidence. So by using this we can calculate the answer.

Formula used: In the solution we will be using the following formula,
$\Rightarrow {\theta _i} = {\theta _r}$ where ${\theta _i}$ is the angle of incidence and ${\theta _r}$ is the angle of reflection from a plane mirror.

Complete step by step answer
In the question we are given the incident ray in the diagram. So on completing the figure we get,

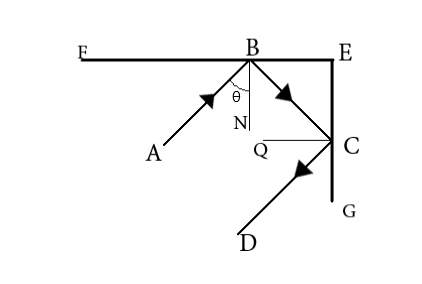
The incoming incident ray AB has an angle ${\theta _i}$. After reflection, the law of reflection dictates that the reflected ray BC has an angle of reflection equal to the angle of incidence.
Hence from diagram angle $\angle NBC = \angle ABN = {\theta _i}$.
Thus, in general, angle $\angle ABC = {\theta _i} + {\theta _i} = 2{\theta _i}$.
From a rule of geometry, alternate angles are equal. Therefore, the angles $\angle BCE$ and $\angle NBC$ are alternate angles so we can write,
$\Rightarrow \angle BCE = \angle NBC$
Since $\angle NBC = {\theta _i}$ then we get $\angle BCE = {\theta _i}$
The line QC is the normal of the mirror EG, hence angle $\angle QCE = 90^\circ$
Then $\angle BCQ = 90^\circ - \angle BCE$.
Replacing $\angle BCE = {\theta _i}$ into equation above, we have that
$\Rightarrow \angle BCQ = 90^\circ - {\theta _i} = \alpha$
Now, we see that the line BC which is the reflected ray of mirror FE is the incident ray of mirror EG. Hence, $\angle BCQ = \alpha$ is the angle of incidence of mirror EG.
Also, in a vertical plane mirror, the angle of incidence is equal to the angle of reflection.
Hence,
$\Rightarrow \angle QCD = \alpha$
Then, in total,
$\Rightarrow \angle BCD = \alpha + \alpha = 2\alpha$
Line $ECG$ can be regarded as an angle on a straight line which is equal to $180^\circ$
Hence, angle $\angle DCG = 180 - 2\alpha - {\theta _i} = 180 - 2(90 - {\theta _i}) - {\theta _i}$
Evaluating, we have the value as,
$\Rightarrow \angle DCG = 180 - 180 + 2{\theta _i} - {\theta _i}$
So we get,
$\Rightarrow \angle DCG = {\theta _i}$
We see that irrespective of incident angle ${\theta _i}$ the emergent ray always makes the same angle ${\theta _i}$ with the vertical. Hence, AB is parallel to DC irrespective of angle of incidence.
Thus, the correct option is (D).

Note
A common error is for students to think that because ray AB is parallel to ray DC, the shape ABCD must be part of a rectangle. However, this is erroneous. To circumvent such error, we need to think as follows: if angle ${\theta _i}$ is, say $60^\circ$ the angle of reflection is also $60^\circ$, then angle $\angle ABC = 120^\circ$ but a corner of a rectangle is equal to $90^\circ$, hence line ABCD must not always be a rectangle.