Question
Question: Two plane mirrors are inclined to one another at an angle of \(60^\circ \). A ray is incident on mir...
Two plane mirrors are inclined to one another at an angle of 60∘. A ray is incident on mirror M1 at an angle i. The reflected ray from mirror M2 is parallel to mirror M1 as shown in figure. The angle of incidence i is:
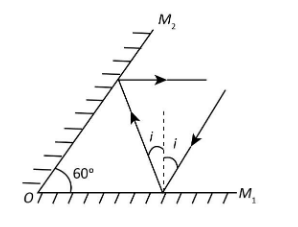
Solution
First, we will draw the ray diagram according to the given conditions. We will then find the angle made by the reflected ray from the mirror M2 with the plane of the mirror using the corresponding angle property. The normal is perpendicular to the mirror surface. We will apply this property along with the law of reflection equating the angles of incidence and reflection, and the properties of triangles and angles in the diagram to find the incident angle.
Complete answer:
The reflected ray from the mirror M2 is given to be parallel to the mirror M1. It is also given that the mirrors M1 and M2 are inclined at an angle 60∘ with each other.
Therefore, the figure corresponding to the given case can be drawn as follows.
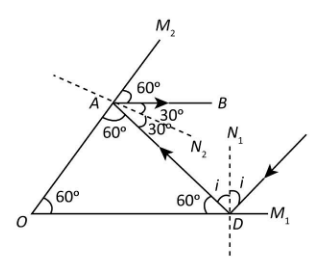
As we can see from the figure, ∠M2AB is the corresponding angle of ∠M2OM1. Therefore,
⇒∠M2AB=∠M2OM1=60∘
Now, the lineAN2 represents the normal to the mirror M2. Since the normal makes an angle 90∘ with the plane of the mirror M2, we can write
∠M2AN2=90∘
It implies,
∠BAN2 is the angle of reflection of the ray from the mirror M2. Since the angle of reflection equals the angle of incidence on a plane mirror, the angle of incidence of the ray on the mirror M2 is, ∠N2AD=30∘. Therefore, we get
∠N2AO=90∘
It implies,
We know that in , the sum of all the angles is equal to 180∘. Therefore,
∠DAO+∠AOD+∠ODA=180∘ ⇒60∘+60∘+∠ODA=180∘ ⇒∠ODA=60∘
We know that the angle of incidence of the ray on the mirror M1 is i. Since the angle made by the normal N2D with the plane of the mirror is 90∘, we can write
∠ODA+∠ADN2=90∘ ⇒60∘+i=90∘ ∴i=30∘
Therefore, the angle of incidence i is 30∘.
Note: It is to be noted that the normal is a line drawn perpendicular to the surface of a mirror. The angles made by the reflected ray with the normal and the incident ray with the normal are always equal. Also, in questions of this type where it is given that the two mirrors are inclined at an angle θ, and the incident ray on the first mirror reflects from the second mirror parallel to the first, the incident ray angle i is 2θ−90∘. So, the incident angle can be found directly without doing many steps.
