Question

Two plane mirrors are inclined to each other at an angle of ${60^ \circ }$. If a ray of light incident on the first mirror is parallel to the second mirror, it is reflected from the second mirror
A.Perpendicular to the first mirror
B. Parallel to the first mirror
C. Parallel to the second mirror
D. Perpendicular to the second mirror

Answer 1

In this question, we will use the property that the angle of incidence and the angle of reflection is always equal for a plane mirror. Draw the figure first using the given information and then using trigonometry try to find the required angle.

Complete step by step answer:
Let’s first write down the given information:
The mirrors are at an angle of ${60^ \circ }$ with respect to each other.
The ray of light incident on the first mirror is parallel to the second mirror.
Let us first draw the diagram as mentioned in the question. Let the incident ray be denoted as ‘i‘ and the reflected ray be denoted as ‘r’.

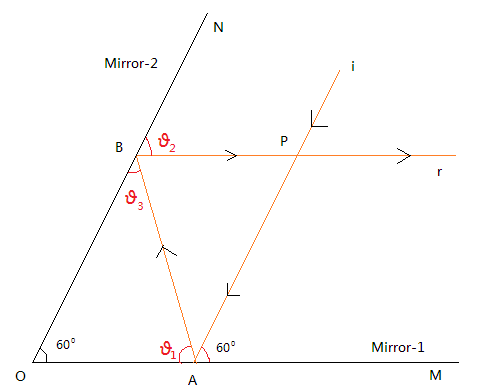
Here we have two mirrors and the incident ray ‘i’ is parallel to the second mirror ‘Mirror-2’.
From the diagram, we have;
$\angle PAM = {60^ \circ }$ --equation $1$
As the incident ray is parallel to the second mirror and the mirrors are placed at an angle of ${60^ \circ }$
$\angle BOA = {60^ \circ }$ as per given information.
In order to answer the question, we need to find the angle ${\theta _2}$. If ${\theta _2} = {60^ \circ }$ then we can easily say that the reflected ray is parallel to the first mirror. So, lets find the angle ${\theta _2}$.
In $\vartriangle BOA$, we have $\angle BOA = {60^ \circ }$ as per given information,
As we know that the angle of incident and the angle of reflection is equal for a plane mirror. Therefore, we can have;
$\angle PAM = \angle BAO$
$\Rightarrow \angle BAO = {\theta _2} = {60^ \circ }$ -from equation $1$ $\Rightarrow {\theta _3} = \angle OBA = {60^ \circ }$ as sum of angles of a triangle is ${180^ \circ }$
For the reflected ray, we have ${\theta _2} = {\theta _3}$ as angle of incidence and angle of reflection for the reflected ray.
${\theta _2} = {60^ \circ }$
Now as $\angle NBP = \angle OBA$, so conversely, we can say that;
The reflected ray BP is parallel to first mirror (Mirror-1)

So, the correct answer is “Option B”.

Note:
Calculate the angles properly. The angle of incidence and angle of reflection will always be equal in the case of a plane mirror.
It is easier to solve this problem once the diagram is drawn. If light hits a plane mirror perpendicularly, the light will trace the same path after reflection.