Question

Two plane mirrors are inclined at angle $\theta$ as shown in figure. If a ray parallel to OB strikes other mirror at P and finally emerges parallel to OA after two reflections then $\theta$ is equal to

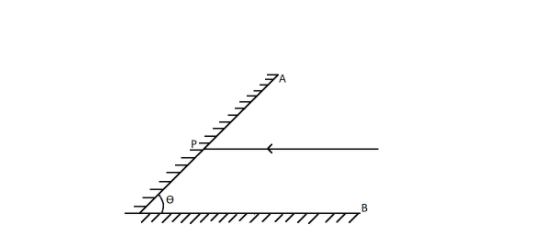
(A) $90^\circ$
(B) $60^\circ$
(C) $45^\circ$
(D) $30^\circ$

Answer 1

Hint We need to first complete the given ray the diagram in which the incident ray falls on the second mirror parallel to the first mirror and the final reflected ray is parallel to the second mirror. So if we consider the angle between the mirrors as $\theta$ then from the geometry of the diagram, we can find the value of $\theta$.

Complete Step by Step Solution
In the question it is said that the incident ray falls on the first mirror A parallel to the second mirror B. So if the angle of inclination between the two mirrors as $\theta$, then the angle which the incident ray makes with the mirror A is $\theta$. Similarly we are given that the final reflected ray from the mirror B is parallel to the mirror A. So we get the angle that the reflected ray makes with the mirror B is again $\theta$.
So we can draw the raw diagram as,

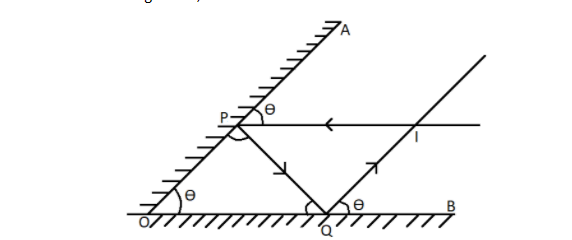
Here IP is the incident ray and QI is the reflected ray. The angle $\angle POQ$ is the angle between the mirrors equal to $\theta$. Now as the angle with which IP falls on A is $\theta$. So from geometry, $\angle OPQ$ is also equal to $\theta$. And similarly the angle which QI makes with B is $\theta$. So again from geometry, $\angle OQP$ is also equal to $\theta$. So in the triangle $\Delta POQ$, the three angles are $\theta$ each.
Now the sum of all the angles in a triangle is $180^\circ$. So we can write,
$\theta + \theta + \theta = 180^\circ$
Adding the LHS we get
$3\theta = 180^\circ$
So on dividing both the sides with 3,
$\theta = \dfrac{{180^\circ }}{3} = 60^\circ$
Therefore the angle between the mirrors A and B is $60^\circ$.

So the correct answer is option B.

Note During the reflection of a ray of light in a mirror, according to the laws of reflection, the angle of incidence is equal to the angle of reflection. So this is why we have taken the angles $\angle OPQ$ and $\angle OQP$ as $\theta$ from geometry.