Solveeit Logo
Login

Question

Question: Two plane mirrors are inclined at an angle \(\theta \) Light ray is incident parallel to one of the ...

Two plane mirrors are inclined at an angle θ\theta Light ray is incident parallel to one of the mirrors. For what value of θ\theta ray will retrace its path after the third reflection?

Explanation

Solution

In order to solve this question, we will first draw the diagram to show the path of light and then using geometry of lines and angles we will find the value of θ\theta for which light will retrace its path after third reflection, also a light ray only retrace its path after reflection if it incident normally to the mirror.

Complete step by step answer:
Let us first draw a diagram in which PM and PN are two mirrors inclined at an angle θ\theta and a light ray AB parallel to one of mirror say MN incident on mirror PM with angle of incidence θ\theta at point B and then the second reflection of light ray takes place on mirror MN at point C and then after third reflection of light ray takes place on mirror PM at point D normally and due to normal incidence light ray will retrace it’s path back as shown in the diagram.

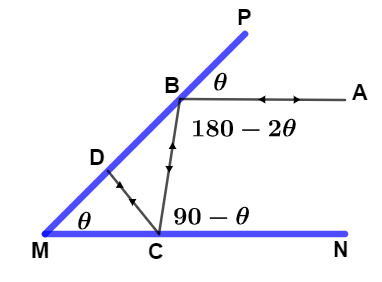
From the diagram’s geometry we see that,
∠CDM=90o\angle CDM = {90^o} so in right angle triangle CDM we have,
∠DCM=90−θ\angle DCM = 90 - \theta which is angle of reflection at point C and
∠BCN=∠DCM=90−θ→(i)\angle BCN = \angle DCM = 90 - \theta \to (i) angle of incidence at point C equals to angle of reflection.
Also,
∠PBA=θ\angle PBA = \theta angle of incidence at point B
∠CBD=∠PBA=θ\angle CBD = \angle PBA = \theta angle of reflection equals to angle of incidence at point B.
Now for straight line PM,
∠PBA+∠ABC+∠CBD=180o\angle PBA + \angle ABC + \angle CBD = {180^o} on putting the values we get,
∠ABC=180−2θ→(ii)\angle ABC = 180 - 2\theta \to (ii)
Now, we see that lines AB∣∣MNAB||MN and BC is a intercept so, by the property of geometry of lines we know that, Sum of angles on same side by intercept line between two lines is 180o{180^o} which can be written as
∠ABC+∠BCN=180o\angle ABC + \angle BCN = {180^o} on putting the value of these angles from equation (i) and (ii) we get,
180−2θ+90−θ=180180 - 2\theta + 90 - \theta = 180
3θ=903\theta = 90
⇒θ=30o\Rightarrow \theta = {30^o}
Hence, two mirrors must be inclined at an angle of 30o{30^o} so that light retraces its path after third reflection.

Note: It should be remembered that, it’s the law of reflection in ray optics that, angle of incidence is always equal to angle of reflection and when a ray of light incident normally on a mirror its angle of reflection and angle of incidence with respect to normal is zero that’s why a light ray retrace its path.