Question

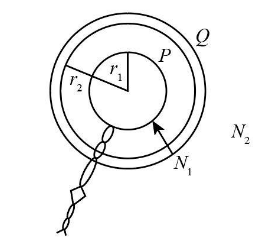
Two plane circular coils P and Q have radii ${r_1}$ and ${r_2}$respectively$({r_1} << {r_2})\;$and are coaxial as shown in fig. The number of turns in P and Q are respectively ${N_1}$and ${N_2}$. If the current in coil Q is varied steadily at a rate x ampere/sec, then the induced EMF in the coil P will be approximately?

(A) ${\mu _0}{N_1}{N_2}\pi r_1^2$
(B) ${\mu _0}{N_1}{N_2}\pi r_1^2$
(C) $\dfrac{{{\mu _0}{N_2}}}{{2{r_2}}} \times {N_1} \times \pi r_1^2 \times x$
(D) $0$

Answer 1

Biot-Savart law provides the value of the magnetic field in a circular loop due to the current in the loop. The value of the magnetic field at the centre of a circular loop can be calculate by the formula $B = \dfrac{{{\mu _0}NI}}{{2r}}$ , here $I$ represents current in the loop, $r$ is the radius of the circular loop, $N$ is the number of turns and ${\mu _0}$ is the permeability of the vacuum. And The EMF induced can be calculated by Faraday's law.

Complete step by step answer:
Let the current ${I_2}$ is flowing in the coil Q
It is given that the current in coil Q is varied steadily at a rate x ampere/sec.
So
$\dfrac{{d{I_2}}}{{dt}} = x\;{{{\rm{ampere}}} {\left/ {\vphantom {{{\rm{ampere}}} {{\rm{sec}}}}} \right. } {{\rm{sec}}}}...........{\rm{(1)}}$
It is given that $({r_1} << {r_2})\;$ so the coil P will act as a centre for coil Q.
The magnetic field at coil Q is given as follows,
${B_Q} = \dfrac{{{\mu _0}{N_2}{I_2}}}{{2{r_2}}}$
This magnetic field will provide magnetic flux in the coil P.
So the magnetic flux in the coil P is
$\phi = {N_1}{B_Q}A$
Here, $A$ is the area of coil P and that is $A = \pi r_1^2$
The value of the EMF induced in coil P will be equal to the rate of change in the magnetic flux in the coil P.
So the EMF in the coil P by using of Faraday's law is,
$\varepsilon = \dfrac{{d\phi }}{{dt}}\\\ \Rightarrow\varepsilon = \dfrac{{d\left( {{N_1}{B_Q}A} \right)}}{{dt}}\\\ \Rightarrow\varepsilon = {N_1}A\dfrac{{d\left( {{B_Q}} \right)}}{{dt}}$
Substitute all the values in the above expression.
$\varepsilon = {N_1}A\dfrac{{d\left( {\dfrac{{{\mu _0}{N_2}{I_2}}}{{2{r_2}}}} \right)}}{{dt}}\\\ \Rightarrow\varepsilon = \dfrac{{{\mu _0}{N_2}}}{{2{r_2}}} \times {N_1}A \times \dfrac{{d{I_2}}}{{dt}}$
Substitute the value of $A$ and the value of $\dfrac{{d{I_2}}}{{dt}}$ from equation (1).
$\therefore\varepsilon = \dfrac{{{\mu _0}{N_2}}}{{2{r_2}}} \times {N_1} \times \pi r_1^2 \times x$

Therefore, the induced EMF in the coil P is $\dfrac{{{\mu _0}{N_2}}}{{2{r_2}}} \times {N_1} \times \pi r_1^2 \times x$ and correct option is option (C).

Note: In such types of questions first find the magnetic field in the first coil then evaluate induced magnetic flux in the second coil and then you can calculate the change in magnetic flux or induced EMF in the second coil.