Question

Two persons are holding a rope of negligible weight tightly at its ends so that it is horizontal. A 15 kg weight is attached to the rope at the midpoint which now no longer remains horizontal. The minimum tension required to completely straighten the rope is:
${\text{A}}{\text{. 15kg}} \\\ {\text{B}}{\text{. }}\dfrac{{15}}{2}kg \\\ {\text{C}}{\text{. 5kg}} \\\ {\text{D}}{\text{. infinitely large}} \\\$

Answer 1

- Hint: The vertical component of tension in the rope is balanced by the weight. In order to regain the original configuration of being parallel to horizontal, the rope needs to make zero angles with the horizontal.

Complete step-by-step solution -
We are given that two persons are holding a rope of negligible weight tightly at either ends such that the rope remains horizontal.
Now, a weight of 10 kg is attached to the rope at its mid-point. Diagrammatically, the situation can be visualized as shown in the diagram.

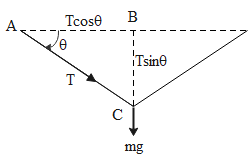
Tension in the rope is due to the weight of 10 kg. We can resolve the components of tension T into $T\sin \theta$ and $T\cos \theta$ where $\theta$ is the angle which the rope makes with the horizontal. The vertical component of tension balances the weight. Therefore we can write the following expression:
$2T\sin \theta = mg{\text{ }} \\\ \Rightarrow T = \dfrac{{mg}}{{2\sin \theta }}{\text{ }}...{\text{(i)}} \\\$
When $\theta = 0^\circ$, the rope is straight. Therefore, in order to bring back the rope to a straight position, i.e. $\theta = 0^\circ$, the tension required to the task can be calculated using $\theta = 0^\circ$in equation (i). We get
$T = \dfrac{{mg}}{{2\sin 0}} = \dfrac{{mg}}{0} = \infty$
This implies that an infinite amount of tension is required to straighten the rope with weight attached to it.
Hence, the correct answer is option D.

Note: 1. The factor 2 is coming in equation (i) because of the two components of tension from the either sides.
2. The equation (i) holds true only when the system has attained equilibrium.
3. The amount of tension required to straighten the rope does not depend on the weight suspended at the midpoint of rope.