Question

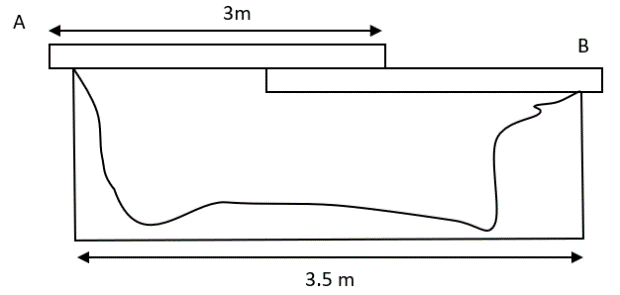
Two persons A and B are standing on the opposite sides of a 3.5-meter wide water stream which they wish to cross. Each of them has a reserved wooden plank whose mass can be neglected, however, each plank is only slightly longer than three meters. So they decide to arrange them together as shown in the figure schematically. With B mass 17 kgs standing, the maximum mass of A who can walk over the plank is close to:

$\begin{aligned} & A.17kg \\\ & B.65kg \\\ & C.85kg \\\ & D.105kg \\\ \end{aligned}$

Answer 1

Hint: For the plank B to be balanced the torque due to all forces around the hinge point should be equal to zero. This is because the plank B should be stable without any rotation so that A can walk over his plank. So calculate the net torque and equate it to zero.

Complete step-by-step answer:
We are given that each plank is 3.5 meters wide and the mass of each plank is negligible.
Let us now consider the arrangement of planks as shown in the figure.

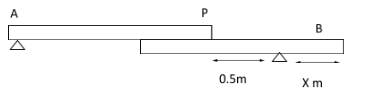
Now the person A can walk on the plank from point A to P and person B is standing at point B

Let us consider the mass of person A as m
The mass of a person B is given as 17 kg
Now the person A walks from point A to the end of his plank and cannot move further.
The free-body diagram of the plank B can be drawn as below

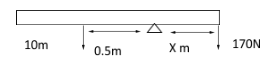
We know that The torque is given by Torque = force $\times$ perpendicular distance
Using the torque formula we can now calculate the net torque acting on the plank due to all forces as below

Net torque is given by 10m(0.5)-170(x) = 0 for stable plank
We get $m = \dfrac{170x}{5}$

So the maximum possible value of the m is obtained when the value of x is maximum
The max value of the x possible is x= 2.5

So we get the value of the $m = \dfrac{170\times 2.5}{5} = 85 kg$

So, in summary, the value of the mass of A that can be possible is given by 85 kg.

Note: The free-body diagram has to be made to get a clear picture of the problem and the condition has to be chosen such that the rotation of the plank does not occur at the hinge . one of the major mistakes made in this kind of problem is that one may tend to take the condition that net force is zero on the plank B which is wrong. We need to see that the plank B is not rotating or in a stable state.