Question

Two particles start together from a point O and slide down along straight smooth wires inclined at ${30^ \circ }{\text{ and }}{60^ \circ }$ to the vertical plane and on the same side of vertical through O. The relative acceleration of second with respect to first will be of magnitude:

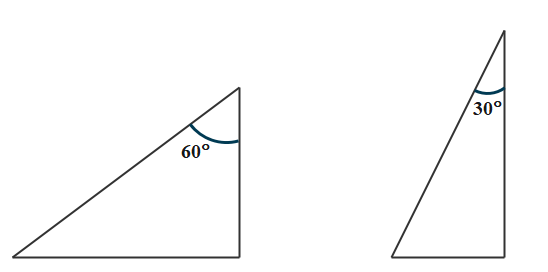
A. $\dfrac{g}{2}$ in the vertical direction
B. $\dfrac{{\sqrt 3 g}}{2}$ at ${45^ \circ }$ with vertical
C. $\dfrac{g}{{\sqrt 3 }}$ inclined at ${60^ \circ }$ to the vertical
D. $g$ in the vertical direction.

Answer 1

Hint: A particle sliding down a smooth surface is free of frictional influence. Deduce the components of forces acting on the ball with help of a suitable example. Then find expression for acceleration and hence calculate the relative acceleration between the two particles by finding the angle between the two.

Formula Used:
The magnitude of relative acceleration:
${a_r} = \sqrt {a_1^2 + a_2^2 - 2{a_1}{a_2}\cos {{30}^ \circ }}$

Complete step by step answer:
When a particle slides down a smooth straight wire inclined to the vertical with angle $\theta$. Then there are a total of two major forces acting on it, which on dividing into their respective components is shown in the figure below:

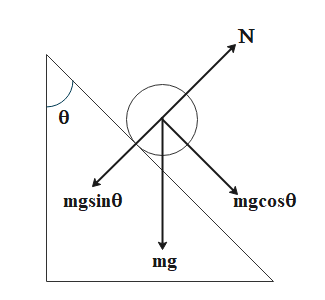
The weight of the particle acts vertically downwards. But, because friction does not come into play for this setup, so the acceleration achieved by the particle is completely the cosine component of its weight. Additionally, the sine component of the weight gets balanced out by the normal reaction force, as they are two equal forces acting in opposite directions.
Mathematically,
$mg\sin \theta = N$
And
\eqalign{ & mg\cos \theta = ma \cr & \Rightarrow a = g\cos \theta \cdots \cdots \cdots \cdots \left( 1 \right) \cr}
Now, let ${a_{1{\text{ }}}}{\text{and }}{a_2}$ be the acceleration of the two particles inclined with vertical at angle ${30^ \circ }{\text{ and }}{60^ \circ }$respectively.
So, from equation (1) we get acceleration for the first particle as:
\eqalign{ & {a_1} = g\cos {30^ \circ } \cr & \Rightarrow {a_1} = \dfrac{{\sqrt 3 g}}{2} \cdots \cdots \cdots \left( 2 \right){\text{ }}\left[ {\because \cos {{30}^ \circ } = \dfrac{{\sqrt 3 }}{2}} \right] \cr}
Similarly, we get acceleration for the second particle as:
\eqalign{ & {a_2} = g\cos {60^ \circ } \cr & \Rightarrow {a_2} = \dfrac{g}{2} \cdots \cdots \cdots \cdots \left( 3 \right){\text{ }}\left[ {\because \cos {{60}^ \circ } = \dfrac{1}{2}} \right] \cr}
Relative acceleration is given by:
${a_r} = \left| {{a_1} - {a_2}} \right|$
Angle between the two accelerations${a_{1{\text{ }}}}{\text{and }}{a_2}$ is given by:
${60^ \circ } - {30^ \circ } = {30^ \circ }$
Thus the relative acceleration of second particle with respect to the first in magnitude will be:
\eqalign{ & {a_r} = \sqrt {a_1^2 + a_2^2 - 2{a_1}{a_2}\cos {{30}^ \circ }} \cr & \Rightarrow {a_r} = \sqrt {{{\left( {\dfrac{{\sqrt 3 g}}{2}} \right)}^2} + {{\left( {\dfrac{g}{2}} \right)}^2} - 2 \times \dfrac{{\sqrt 3 g}}{2} \times \dfrac{g}{2} \times \dfrac{{\sqrt 3 }}{2}} \cr & \Rightarrow {a_r} = \sqrt {\dfrac{{3{g^2}}}{4} + \dfrac{{{g^2}}}{4} - \dfrac{{3{g^2}}}{4}} \cr & \Rightarrow {a_r} = \sqrt {\dfrac{{3{g^2}}}{4} + \dfrac{{{g^2}}}{4} - \dfrac{{3{g^2}}}{4}} \cr & \therefore {a_r} = \dfrac{g}{2} \cr}
Therefore, the correct option is A. i.e., $\dfrac{g}{2}$ in the vertical direction.

Note: Whenever two bodies slip over each other, the force of friction that comes into action is called kinetic friction. But if these bodies do not slide then the force of friction is said to be static friction. Additionally, the frictional force exerted by fluids is known as viscosity.