Question

Two particles start simultaneously from the same point and move along two straight lines, one with uniform velocity $v$ and other with a uniform acceleration $a$. If $\alpha$ is the angle between the lines of motion of two particles, then the least value of relative velocity will be at time given by
$\begin{aligned} & A)\left( \dfrac{v}{\alpha } \right)\sin \alpha \\\ & B)\left( \dfrac{v}{a} \right)\cos \alpha \\\ & C)\left( \dfrac{v}{a} \right)\tan \alpha \\\ & D)\left( \dfrac{v}{a} \right)\cot \alpha \\\ \end{aligned}$

Answer 1

Relative velocity refers to the difference in velocities of two particles at a particular time of consideration. When the first derivative of relative velocity with respect to time is equated to zero, we get the time when relative velocity is in its least possible value.
Formula used:
$1)\overrightarrow{{{v}_{12}}}=\overrightarrow{{{v}_{1}}}-\overrightarrow{{{v}_{2}}}$
$2)\dfrac{d{{v}_{12}}}{dt}=0$

Complete answer:
We are provided that two particles start simultaneously from the same point and move along two straight lines, one with uniform velocity $v$ and other with a uniform acceleration $a$. If $\alpha$ is the angle between the lines of motion of two particles as shown in the figure, we are required to determine the time when the relative velocity of both these particles has the least possible value.

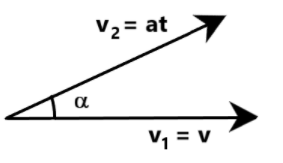
Let us call the uniform velocity of the first particle ${{v}_{1}}$. Clearly,
${{v}_{1}}=v$, as provided in the question
Similarly, let us call the velocity of the second particle ${{v}_{2}}$. Clearly,
${{v}_{2}}=at$
where
$a$ is the uniform acceleration of the second particle, as provided in the question
$t$ is the time at which the velocity is measured
Let this set of equations be denoted as X.
Now, relative velocity of a particle with respect to another particle at a particular time is defined as the difference in velocities of these particles at that particular time. In our question, if $\overrightarrow{{{v}_{12}}}$ denotes the relative velocity of the first particle with respect to the second particle at a particular time, then, $\overrightarrow{{{v}_{12}}}$ is given by
$\overrightarrow{{{v}_{12}}}=\overrightarrow{{{v}_{1}}}-\overrightarrow{{{v}_{2}}}$
where
$\overrightarrow{{{v}_{1}}}$ is the uniform velocity of the first particle
$\overrightarrow{{{v}_{2}}}$ is the velocity of the second particle at the particular time of consideration
Clearly, the magnitude of $\overrightarrow{{{v}_{12}}}$ can be written as
${{v}_{12}}^{2}={{v}_{1}}^{2}-2{{v}_{1}}{{v}_{2}}\cos \alpha +{{v}_{2}}^{2}={{v}^{2}}-2vat\cos \alpha +{{a}^{2}}{{t}^{2}}$
where
${{v}_{12}}$ is the magnitude of relative velocity of the first particle with respect to the second particle at time $t$
$v$ is the uniform velocity of the first particle
$a$ is the uniform acceleration of the second particle
$\alpha$ is the angle between lines of motion of the particles
Let this be equation 1.
Now, to determine the time at which relative velocity of the first particle with respect to the second particle is the least, let us take the first derivative of equation 1 with respect to time $t$ and equate it to zero.
On differentiating equation 1 with respect to time and equating it to zero, we have,
$\dfrac{d{{v}_{12}}^{2}}{dt}=0\Rightarrow \dfrac{2d{{v}_{12}}}{dt}=0\Rightarrow \dfrac{d{{v}_{12}}}{dt}=0\Rightarrow \dfrac{d({{v}^{2}}-2vat\cos \alpha +{{a}^{2}}{{t}^{2}})}{dt}=0$
Let this be equation 2.
On further simplification of equation 2, we have
$\dfrac{d({{v}^{2}}-2vat\cos \alpha +{{a}^{2}}{{t}^{2}})}{dt}=0\Rightarrow -2av\cos \alpha +2{{a}^{2}}t=0\Rightarrow t=\dfrac{v\cos \alpha }{a}$
Therefore, the least value of relative velocity will be at time given by $\left( \dfrac{v}{a} \right)\cos \alpha$.

Hence, the correct answer is option $B$.

Note:
Students need to understand the significance of taking the first derivative of relative velocity with respect to time and equating it to zero. This is given by equation 2 in the above solution for reference. Here, we are calculating the change in relative velocity during a particular time interval. If this change in relative velocity during a particular time is assumed as zero, we get the least value of relative velocity. Thus, we can easily determine the time at which relative velocity is the least.