Question
Question: Two particles, of masses M and 2M, moving, as shown, with speeds of 10m/s and 5m/s, collide elastica...
Two particles, of masses M and 2M, moving, as shown, with speeds of 10m/s and 5m/s, collide elastically at the origin. After the collision, they move along the indicated directions with speeds v1 and v2 respectively. The values of v1 and v2 are nearly?
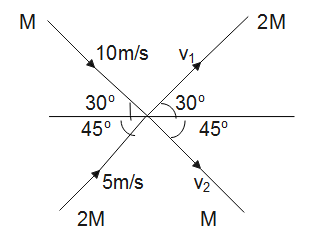
Solution
During the collision of particles having certain masses, law of conservation of mass is used. In this question, we find a relation between the masses and the velocity of the particle. Putting the given values in the expression will give us the required result.
Formula used:
M×10cos30+2M×10cos45
Complete step by step answer:
To find the velocities of the two particles, we have the following relation. Here, particle A with mass M makes an angle of 30 degree, whereas particle B of mass 2M makes an angle of 45 degree. So, our equation becomes:
\eqalign{& M \times 10\sin {30} + 2M \times 5\sin {45} \cr
& = 2M \times {v_1}\cos {30} + M{v_2}\cos {45} \cr}
Now, when we substitute the given values in above equation we get:
53+52=2v123+2v2
Now, after the collision of the two particles, we get the equation as:
\eqalign{
& 10 \times M\sin {30} - 2M \times 5\sin {45} \cr
& = M{v_2}\sin {45} - 2M{v_1}\sin {30} \cr}
Substituting the given values in the above equation we get the required velocities as:
\eqalign{& 5 - 5\sqrt 2 = \dfrac{{{v_2}}}{{\sqrt 2 }} - {v_1} \cr
& \Rightarrow {v_1} = \dfrac{{17.5}}{{2.7}} \approx 6.5m/s \cr
& \therefore {v_2} \approx 6.3m/s \cr}
Therefore, we get the velocities of the particle having mass M and 2M respectively. We can observe that the velocity of the two particles differ in very low value.
Additional information:
From the law of conservation of mass which says that mass can neither be created nor destroyed in any chemical reactions. Also, it can be defined as the mass of any one element at the beginning of a reaction will equal the mass of that element at the end of the reaction.
We know that collision means when two objects come in contact with each other for a very short period. Collision is an interaction between two masses for a very short interval where the momentum and energy of the colliding masses changes. Here are two types of collision: first id elastic collision where the energy remains same after interaction or collision and second is inelastic collision where the final energy changes after the collision of the particles or body.
Note:
The resulting mass, energy or velocity after the collision of two particles depends on its direction and magnitude as well. During the solution, one should see that laws of conservation are not violated, i.e., mass can neither be created nor be destroyed and similarly for energy of the particles as well.
