Question

Two particles of masses $m_1$ and $m_2$, $m_1$ > $m_2$, move in circular paths under the action of their gravitational attraction. Then:
A. They move in the same circle
B. Radius of circular path of $m_1$ is more than that of $m_2$
C. Radius of circular path of $m_1$ is less than that of $m_2$
D. Each moves along circular path of variable radius

Answer 1

The two particles are gravitationally bound to each other, which means they rotate about their effective centre of mass. Using this, determine the distance to the centre of mass for the two particles at equilibrium. This is nothing but the radius of the paths traversed by each particle since the centre of mass becomes their axis of rotation. To this end, arrive at a relationship between the mass and the radius and determine the appropriate result.

Formula used: Distance to centre of mass: $r_1 = d.\dfrac{m_2}{m_1+m_2}$

Complete step by step answer:
We have two particles of mass $m_1$ and $m_2$ such that $m_1$ > $m_2$. These two particles are gravitationally bound and execute an effective circular motion as a gravitationally bound system. In such a case, we know that the axis of rotation of this system will be at the centre of mass of this system. The centre of mass (CoM) is the point where the whole mass of the system seems to be positioned. Since our particles are weighted, the centre of mass will lie closer to the heavier particle since that is where the majority of the mass of the system lies. Thus, both particles move in a circular path due to the mutual gravitational force of attraction with the centre of mass as their axis of rotation.

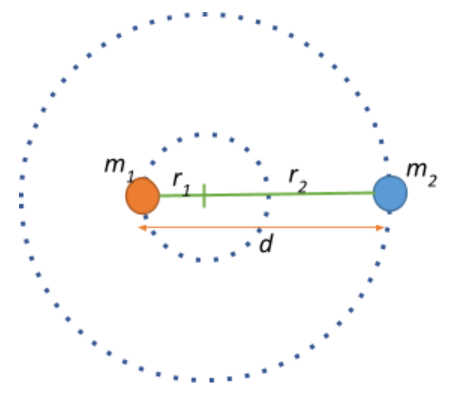
Thus, the centre of mass can be defined as the point where:
$m_1r_1=m_2r_2$, where $r_1$ and $r_2$ are the distance of the CoM from each particle respectively.
$\Rightarrow r_1 = \dfrac{m_2r_2}{m_1}$
We have the distance of separation between the two particles as $d=r_1+r_2$
$\Rightarrow d = \dfrac{m_2r_2}{m_1} +r_2 = r_2.\left(\dfrac{m_2+m_1}{m_1}\right)$
$\Rightarrow r_2 = d.\left(\dfrac{m_1}{m_1+m_2}\right)$
Similarly, $r_1 = d.\left(\dfrac{m_2}{m_1+m_2}\right)$
We have already established that the CoM is the axis of rotation for this system. This means that $r_1$ and $r_2$ are the radius of the circular path executed by $m_1$ and $m_2$ respectively.
Therefore, we have $r_1 \propto m_2$ and $r_2 \propto m_1$.
And since $m_1$>$m_2$, $\Rightarrow r_1$< $r_2$.

So, the correct answer is “Option C”.

Note: Recall that this system is the principle of the dynamics of a binary star system, where two stars gravitationally bound to each other and having comparable masses rotate about their centre of mass established as a result of their gravitational interaction.
Also note that, if the masses of both the particles were the same, then they would both rotate about the same circular path at equal distances from the axis of rotation, i.e.,
If $m_1 =m _2 =m$, then $r_1 = r_2 = \dfrac{d}{2}$, which would subtend the same circular path as a result of their motion.