Question

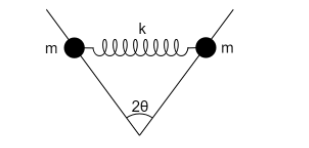
Two particles of mass $m$ are constrained to move along two horizontal frictionless rails that make angle $2\theta$ with respect to each other. They are connected by a spring with spring constant $k$. The angular frequency of oscillations for the motion where the two masses always stay parallel to each other (that is the distance between the meeting point of the rails and each particle is equal) is

(A) $\sqrt {\dfrac{{2k}}{m}}$
(B) $\sqrt {\dfrac{{2k}}{m}} \sin \theta$
(C) $\sqrt {\dfrac{{2k}}{m}} \cos \theta$
(D) $\sqrt {\dfrac{k}{{2m}}} \sin \theta$

Answer 1

Since the motion of the particles is constrained, they are only free to move through the passage. To solve it, we first draw the free body diagrams of the masses and equate the forces acting on the particles with their acceleration. The acceleration is then replaced with the formula containing angular frequency of the motion.

Complete Step by step solution:
It is given in the question that,
The mass of both particles is $m$,
The spring constant of the spring is $k$,
The angle between the paths followed by both particles is $2\theta$,
It is also given that the arrangement is kept horizontal, which means that gravity does not play a role in the motion inside the system.
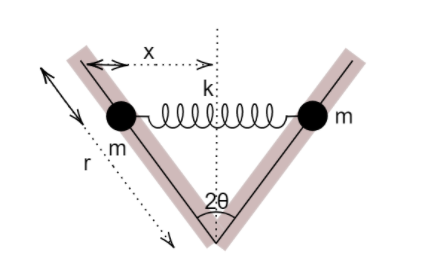
The distance between the masses becomes zero when the spring is compressed completely, whereas it becomes maximum when the spring is stretched, let the distance between both these points be $r$. We need to find the angular frequency of this motion when both particles have a displacement of $r$.
Corresponding to the motion of the masses, the spring compresses and stretches back to its original length, thus a change in the length of spring occurs which is equal to $x$.
The relation between $r$ and $x$ is given by,
$x = r\sin \theta$ $...(A)$
The following diagram makes it clear-

Now consider a particle, it experiences two forces. One is the restoring force of the spring that acts in the X axis and is equal to $kx\;$
The other is the normal contact force$\left( N \right)$ that acts along the walls, perpendicular to the path of the particle.
The particle accelerates through the constrained path.
The free body diagram looks like-

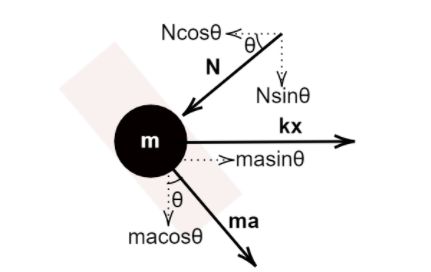
Resolving all the forces in X and Y direction and equating the sum of all forces with the acceleration of the particle, we have-
In X direction,
$ma\sin \theta = kx - N\cos \theta$ $...(B)$
In the Y direction,
$ma\cos \theta = N\sin \theta$ $...(C)$
Substituting the value of $N$ from equation $(C)$,
$N = \dfrac{{ma\cos \theta }}{{\sin \theta }}$
in equation $(B)$,
$ma\sin \theta = kx - \left( {\dfrac{{ma\cos \theta }}{{\sin \theta }} \times \cos \theta } \right)$
$\Rightarrow ma\sin \theta = kx - \left( {\dfrac{{ma{{\cos }^2}\theta }}{{\sin \theta }}} \right)$
Rearranging,
$kx = ma\left( {\sin \theta + \dfrac{{{{\cos }^2}\theta }}{{\sin \theta }}} \right)$
$kx = \dfrac{{ma}}{{\sin \theta }}\left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right)$
We know that, ${\sin ^2}\theta + {\cos ^2}\theta = 1$
Therefore,
$kx = \dfrac{{ma}}{{\sin \theta }}$
$\Rightarrow ma = kx\sin \theta$
This was the force responsible for motion of one particle, for both particles the force is two times.
$ma = 2kx\sin \theta$
$\Rightarrow a = \dfrac{{2kx\sin \theta }}{m}$
We know that angular frequency $\left( \omega \right)$ is related to acceleration as,
$a = {\omega ^2}r$
Where $r$ is the instantaneous displacement of an object exhibiting SHM.
For this question, $r$is the displacement of the particles in their paths.
Therefore,
${\omega ^2}r = \dfrac{{2kx\sin \theta }}{m}$
Substituting value of $x$ from equation $(A)$,
${\omega ^2}r = \dfrac{{2k\left( {r\sin \theta } \right)\sin \theta }}{m}$
$\Rightarrow {\omega ^2}r = \dfrac{{2kr{{\sin }^2}\theta }}{m}$
$\Rightarrow {\omega ^2} = \dfrac{{2k{{\sin }^2}\theta }}{m}$
Solving this,
$\Rightarrow \omega = \sqrt {\dfrac{{2k{{\sin }^2}\theta }}{m}}$
$\Rightarrow \omega = \sqrt {\dfrac{{2k}}{m}} \sin \theta$

Therefore, option (2) is the correct answer.
Note: In the question, we have to find the angular frequency of the motion of the particles, not the angular frequency of the spring. This is why the value of $x$ is substituted with $r$, and the acceleration is taken equal to $a = {\omega ^2}r$.