Question

Two particles of equal mass $m$ are projected from the ground with speeds ${V_1}\,and\,{V_2}$ ​ at angles ${\theta _1}\,and\,{\theta _2}$ ​ as shown in the figure. Given ${\theta _2} > {\theta _1}$ and ${V_1}\cos {\theta _1} = {V_2}\cos {\theta _2}$ ​. Which statement/s is/are correct?

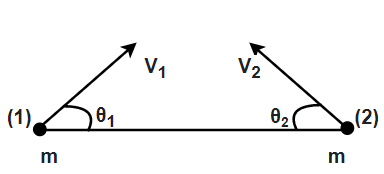
A. $\left( a \right)$ Center of mass of particles will move along a vertical line.
B. $\left( b \right)$ Center of mass of particles will move along a line inclined at some angle with vertical.
C. $\left( c \right)$ Particles $T$ will be above center of mass level when both particles are in air.
D. $\left( d \right)$ Particles $2$ will be above center of mass level when both particles are in air.

Answer 1

Here in this question we have the two particles of the same mass and for this, we will first find the center of the mass of both the particles and from there by using the concept of horizontal and vertical velocity we will be able to get to the solution.

Complete step by step answer:
So in the question, we have the projected velocities of the two particles and are named as ${V_1}\, and\,{V_2}$ .
Since, from the question we have ${\theta _2} > {\theta _1}$ and ${V_1}\cos {\theta _1} = {V_2}\cos {\theta _2}$ .
Therefore, from the velocity of the center of mass of both the particles,
$\Rightarrow {V_{COM}} = \dfrac{{m{V_1}\cos {\theta _1} - m{V_2}\cos {\theta _2}}}{{2m}}$
And by using the above relation, we will get the value from the above equation as
$\Rightarrow {V_{COM}} = 0$
Hence, from this, the center of mass of the particles will move in a vertical line.
Again, as in the question, it is given that ${\theta _2} > {\theta _1}$ , so from this, the particle $2$ will have a greater horizontal velocity and hence will be above the center of the mass level.
Hence, the Center of a mass of particles will move along a line inclined at some angle with vertical. And particles $T$ will be above the center of mass level when both particles are in the air.
Therefore, the option $\left( a \right)\,and\,\left( d \right)$ is correct.

Note: So if we need to define the COM, then it will be as the center of mass of a conveyance of mass in space is the unique point where the weighted relative situation of the dispersed mass is added to zero. This is the highlight which a force might be applied to cause a straight increasing speed without an angular acceleration.