Question
Question: Two particles of equal mass are projected simultaneously with speeds \( 20m/s \) and \( 10\sqrt 3 m/...
Two particles of equal mass are projected simultaneously with speeds 20m/s and 103m/s as shown in the figure. Find the maximum height reached by the centre of mass of the particles.
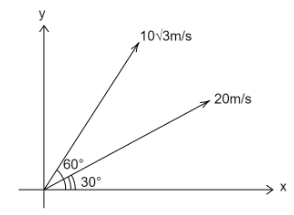
(A) 425m
(B) 1675m
(C) 16125m
(D) 4125m
Solution
To determine the maximum height of the centre of mass of the two particles, we first determine the velocity of the centre of mass of the two particles. We can then take its vertical component and determine its maximum height.
Complete Step by step solution
The first step is to find the vertical component of the velocities of both particles.
We know that the vertical component of a velocity is given by the sine component of that velocity.
Therefore, for the first particle (say particle A ),
The velocity of the body is, vA=103m/s
The angle of projection of the body is, θ=60∘
Thus, the vertical component of the velocity is-
vAY=vAsinθ
It is known that sin60∘=23
Putting the values,
vAY=103×23
⇒vAY=15m/s
Now for the other particle (say particle B )
Particle B has a velocity, vB=20m/s
It is projected at an angle of ϕ=30∘
The vertical component of velocity is given by,
vBY=vBsinϕ
It is known that sin30∘=21
Putting the values,
vBY=20×21
⇒vBY=10m/s
The vertical velocity of the centre of mass of both particles can be given by the equation,
vCY=mA+mBvAYmA+vBYmB
It is given in the question that both particles have the same mass, let m be the mass of both particles, then the equation becomes-
vCY=m+mvAYm+vBYm
Upon taking m common we get,
⇒vCY=2mm(vAY+vBY)
⇒vCY=2vAY+vBY
Putting the value of the velocities,
vCY=215+10
vCY=225m/s
This is the velocity of the centre of mass of both particles in the vertical direction.
The maximum height reached by it is given by,
H=2gvCY2
where g is the acceleration due to gravity., which is taken equal to 10ms−2 .
Putting the values in this equation,
H=2×10(25/2)2
H=8×10625
The maximum height reached by the centre of mass of the particles is 16125m .
Hence, option (C) is correct.
Note
In the question, we have done the calculations using only the vertical velocities of the particles and the centre of mass. This reduces the complexity of questions from calculations involving motion in a plane to motion in a straight line.
