Question

Two particles move in a uniform gravitational field with an acceleration $g$ . At the initial moment the particles were located over a tower at one point and moved with velocities $v = 3\,m{s^{ - 1}}$ and $v = 4\,m{s^{ - 1}}$ horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular.
A. $2.5\,m$
B. $5\,m$
C. $8\,m$
D. none of the above

Answer 1

This question utilizes the concept of projectile motion and gravitational fields. First we need to find their velocities after time $t$ , when they are mutually perpendicular. Then at that point, their dot product becomes zero and we get the value of $t$ . After that, we multiply the time with their relative velocities in the horizontal axis.

Formulae used:
$v = u + at$
where $v$ is the final velocity, $u$ is the initial velocity, $a$ is the acceleration and $t$ is the time taken.

Complete step by step answer:

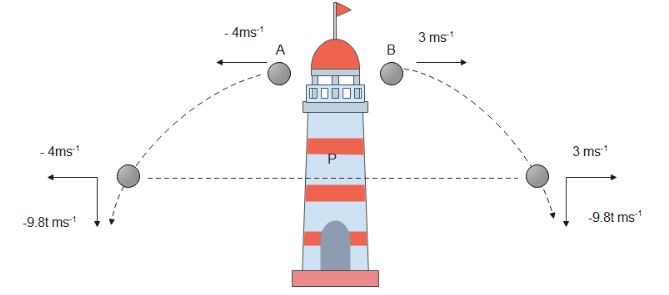
Let there be two particles $A$ and $B$ with velocities $- 4m{s^{ - 1}}$ and $3m{s^{ - 1}}$ respectively. Here, we are taking the velocity of $B$ along the positive $x$ axis. Then the direction of $A$ is opposite to that of $B$ , thus $A$ is given a negative sign.

For particle $A$,
Initial velocity $\overrightarrow {{u_1}} = - 4m{s^{ - 1}}{\kern 1pt} \hat i$
We know that $v = u + at$ , here $a = - g$ (since acceleration due to gravity works downwards, i.e. in the negative quadrant of $y$ axis, thus $g$ is given negative sign here)
Thus velocity becomes

\Rightarrow \overrightarrow {{v_1}} = - 4\hat i - 9.8t{\kern 1pt} \hat j \\\ $$ Similarly, for particle $B$ , $\overrightarrow {{u_2}} = 3m{s^{ - 1}}\hat i$ and $\Rightarrow \overrightarrow {{v_2}} = 3\hat i - 9.8t{\kern 1pt} \hat j$ Let there be a point $P$ where the velocity vectors of both the particles are perpendicular to each other. At that point, the dot product of their velocities becomes zero. Thus, we have $ \Rightarrow \overrightarrow {{v_1}} \cdot \overrightarrow {{v_2}} = 0$ Substituting the values, we get $ \Rightarrow \left( { - 4\hat i - 9.8t{\kern 1pt} \hat j} \right) \cdot \left( {3\hat i - 9.8t{\kern 1pt} \hat j} \right) = 0 \\\ \Rightarrow - 12 + 96.04{t^2} = 0 \\\ \Rightarrow 96.04{t^2} = 12 \\\ \Rightarrow {t^2} = \dfrac{{12}}{{96.04}} \\\ \Rightarrow t = \sqrt {0.1249} \\\ $ Now, we know that the horizontal velocity does not change.Thus, the distance $D$ between the particles when their vectors are mutually perpendicular $ \Rightarrow D = {v_{12}}{\kern 1pt} t$ where ${v_{12}}$ is the relative velocity between particles $1$ and $2$. $ \Rightarrow D = 3 - ( - 4) \cdot \sqrt {0.1249} $ $\Rightarrow D = 7 \times \sqrt {0.1249} \\\ \Rightarrow D = 2.47\,m $ After rounding off, $ \Rightarrow D = 2.5\,m$ **Therefore, the correct option is A.** **Note:** Here, we could have taken $g$ as positive. That would give us the same answer. But since we were following Cartesian sign convention, we stuck with $g$ as negative. Also, you must remember that dot product of a vector works in the following manner $\left( {a\hat i + b{\kern 1pt} \hat j} \right) \cdot \left( {c\hat i + d{\kern 1pt} \hat j} \right) = (a \times c)\hat i + (b \times d)\hat j$. Do not confuse the dot product of the vector with the cross product.