Question
Question: Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separa...
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle systems is the same whatever be the point about which the angular momentum is taken.
Solution
Hint – To get this problem solved we will find the angular momentum about all the possible points and if we get them same then our problem is solved.
Formula Used – Angular momentum = mass x speed x distance between particle and axis about which it is being calculated.
Complete step-by-step answer:
We know that angular momentum can be written as mvr.
We will draw a figure and illustrate from the figure to solve this problem.
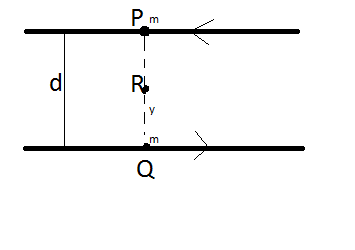
Let two particles be at points P and Q at a given time, as seen in the figure below.
Take point R, which is at a distance from point Q, i.e.
QR = y
PR = d−y
Angular momentum about the point P can be calculated as:
Lp = mv x 0 + mv × d = mvd ......(i)
Angular momentum about the point Q can be calculated as:
L q= mv x d + mv x 0 = mvd....(ii)
Angular momentum about the point R can be calculated as:
Lr = mv x (d−y) + mv x y = mvd ....(iii)
Comparing equations (i), (ii), and (iii), we get:
LP=LQ=LR......(iv)
We assume from equation (iv) that the angular momentum of the device does not depend on the point at which it is taken.
We can easily see that the vector angular momentum of the two particle systems is the same, regardless of the point at which the angular momentum is obtained.
Note – To solve this problem, we measured the angular momentum of all points and found that all points are the same, such that we can assume that the angular vector momentum of the two particle systems is the same, regardless of the point from which the angular momentum is taken.
