Question
Question: Two particles describe the same particles of circle \(R\) in the same direction with the same speed ...
Two particles describe the same particles of circle R in the same direction with the same speed V, then at given instant the relative angular velocity of 2 with respect to 1 will be given as,
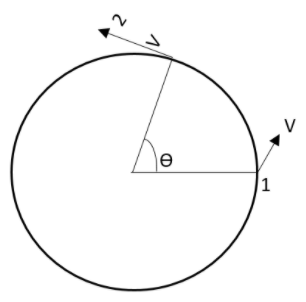
A.R2Vsin2θB.2Rsin2θVC.RVD.RVcos2θ
Solution
First of all find out the velocity at each point and take the relative velocity of 2 with respect to 1. The angular velocity can be found by taking the ratio of the relative velocity of the particle to the radius of the circle. Using this find the angular velocity and arrive at its magnitude. Simplify the equation and find out the correct answer. This will help you in answering this question.
Complete step by step solution:
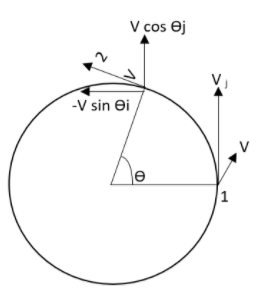
The velocity at 2 is given as,
V2=(vcosθ)j^−vsinθi^
The velocity at 1 has been mentioned as,
V1=vj^
The relative velocity can be found by taking the difference of the velocity at 2 and the velocity at 1. This can be shown as,
V21=V2−V1
Substituting the values in it will give,
V21=(vcosθ)j^−vsinθi^−vj^
The angular velocity can be found by taking the ratio of the relative velocity to the radius of the circle,
ω=RV21=R(vcosθ−v)j^−vsinθi^
The magnitude of the angular velocity can be found as,
ω=Rv(cosθ−1)2+(−sinθ)2
Simplifying this value can be shown as,
ω=Rvcos2θ+1−2cosθ+sin2θ
That is we can write that,
ω=Rv2−2cosθ⇒ω=Rv2(1−cosθ)⇒ω=Rv2×2sin22θ
Therefore we can write that,
ω=R2vsin2θ
Therefore the angular velocity has been calculated.
The correct answer has been mentioned as option A.
Note: Angular velocity is defined as the measure of the speed of an object revolves or rotates relative to another point. That is how fast the angular position or arrangement of an object varies with time. There are two kinds of angular velocity. They are the orbital angular velocity and spin angular velocity. Angular velocity is a vector quantity which is having a magnitude as well as direction.
