Solveeit Logo
Login

Question

Question: Two particles are simultaneously projected in the horizontal direction from a point P at a certain h...

Two particles are simultaneously projected in the horizontal direction from a point P at a certain height. The initial velocities of the particles are oppositely directed to each other and have magnitude v each. The separation between the particles at a time when their position vectors (drawn from the point P) are mutually perpendicular, is
A. v22g\dfrac{{{v^2}}}{{2g}}
B. v2g\dfrac{{{v^2}}}{g}
C. 4v2g\dfrac{{4{v^2}}}{g}
D. 2v2g\dfrac{{2{v^2}}}{g}

Explanation

Solution

When two vectors are A→\overrightarrow A and B→\overrightarrow B are perpendicular to each other then, A→ . B→=0\overrightarrow A \,.\,\overrightarrow B = 0. The rate at which the two particles separate is known as velocity of separation.

Complete step by step solution:

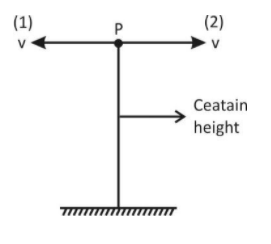
Let two particles named (1) and (2) respectively, are projected direction from point P with same velocity v but opposite in direction. Let after time t’ the position vector of particle (1) and (2) are perpendicular with respect to point P’ then the horizontal velocity tends to separate them and gravity moves in downward direction. So the position vector of particle (i) is given by,
r1→=r→x1+r→y1\overrightarrow {{r_1}} = {\overrightarrow r _{x1}} + {\overrightarrow r _{y1}}
Where r→x1{\overrightarrow r _{x1}} is displacement covered by particle 11in horizontal/xx direction and r→y1{\overrightarrow r _{y1}} is displacement covered by particle 11 in vertical/yy direction.
r1→=vt(−i^)+(0×t+12gt2)(−j^)\overrightarrow {{r_1}} = vt\left( { - \widehat i} \right) + \left( {0 \times t + \dfrac{1}{2}g{t^2}} \right)\left( { - \widehat j} \right)
r1→=−vti^−12gt2j^......(i)\overrightarrow {{r_1}} = - vt\widehat i - \dfrac{1}{2}g{t^2}\widehat j......\left( i \right)
Now the position vector of second particle is given by,

r2→=r→x2+r→y2\overrightarrow {{r_2}} = {\overrightarrow r _{x2}} + {\overrightarrow r _{y2}}
Where r→x2→{\overrightarrow r _{x2}} \to displacement of particle 22 in horizontal/xx direction and r→y2→{\overrightarrow r _{y2}} \to Displacement of particle 22 in vertical/yy direction.
So, r2→=vt(+i^)+(0+12gt2)(−j^)\overrightarrow {{r_2}} = vt\left( { + \widehat i} \right) + \left( {0 + \dfrac{1}{2}g{t^2}} \right)\left( { - \widehat j} \right)
r2→=vti^−12gt2j^\overrightarrow {{r_2}} = vt\widehat i - \dfrac{1}{2}g{t^2}\widehat j
If r→1+r→2{\overrightarrow r _1} + {\overrightarrow r _2} after time ‘t’ thenr→1−r→2=0{\overrightarrow r _1} - {\overrightarrow r _2} = 0
⇒(−vti^−12gt2j^)(vti^−12gt2j^)=0\Rightarrow \left( { - vt\widehat i - \dfrac{1}{2}g{t^2}\widehat j} \right)\left( {vt\widehat i - \dfrac{1}{2}g{t^2}\widehat j} \right) = 0
⇒(vt)2+(12gt2)2=0\Rightarrow {\left( {vt} \right)^2} + {\left( {\dfrac{1}{2}g{t^2}} \right)^2} = 0
⇒(12gt2)2=(vt)2\Rightarrow {\left( {\dfrac{1}{2}g{t^2}} \right)^2} = {\left( {vt} \right)^2}taking underfoot of both sides,
⇒(12gt2)2=(vt)2\Rightarrow \sqrt {{{\left( {\dfrac{1}{2}g{t^2}} \right)}^2}} = \sqrt {{{\left( {vt} \right)}^2}}
⇒12gt2=vt\Rightarrow \dfrac{1}{2}g{t^2} = vt
⇒gt2=v⇒t=2vg\Rightarrow \dfrac{{gt}}{2} = v \Rightarrow t = \dfrac{{2v}}{g}
Now the velocity of separation of the particle (1) and (2)
=v+v=2v= v + v = 2v so the separation between the particles at a time when their position vectors (drawn from the point P) are mutually perpendicular, is
AB ==Velocity of separation ×\timestime
AB =(2v)×t=2v×2vg = \left( {2v} \right) \times t = 2v \times \dfrac{{2v}}{g}
AB =4v2g = \dfrac{{4{v^2}}}{g}

Hence, option (C) is correct.

Additional Information: The velocity of separation or approach is a component of relative velocity of one particle with respect to another.

Note: In this question the horizontal velocity makes effort to move the horizontal direction and that of gravity in downward direction so the displacement into particles is due to both.