Question

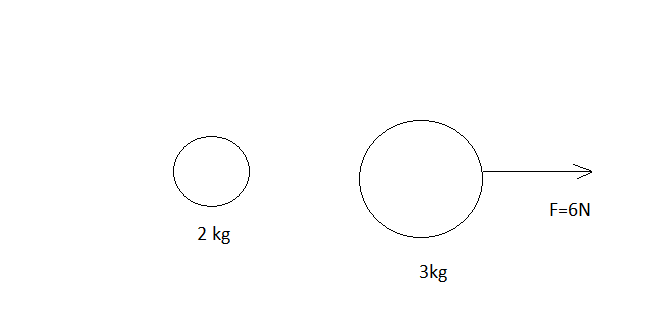
Two particles are shown in the figure. At $t = 0$ , a constant force $F = 6\,{\text{N}}$ starts acting on the $3\,{\text{kg}}$ mass. Find the velocity of the centre of mass of these particles at $t = 5\,{\text{s}}$ .

A. $5\,{\text{m/s}}$
B. $4\,{\text{m/s}}$
C. $6\,{\text{m/s}}$
D. $3\,{\text{m/s}}$

Answer 1

First of all, we will find out acceleration of the bigger body by applying the principle of conservation of momentum. We will substitute the values and manipulate accordingly. Remember both the bodies were initially at rest.

Complete step by step answer:
In the given problem,
Mass of the smaller object is ${\text{2}}\,{\text{kg}}$ .
Mass of the bigger object is $3\,{\text{kg}}$ .
The magnitude of force which acts on the bigger object is $6\,{\text{N}}$ .
Time duration is given as $5\,{\text{s}}$ .

For this, we will first, find the acceleration of the bigger body:
We have a formula, from Newton’s second law of motion:
$F = ma$ …… (1)
Where,
$F$ indicates force acting on the body.
$m$ indicates mass of the body.
$a$ indicates acceleration of the body.
Substituting the required values in the equation (1), we get:
$F = ma \\\ 6 = 3 \times a \\\ a = \dfrac{6}{3}\,{\text{m}}{{\text{s}}^{ - 2}} \\\ a = 2\,{\text{m}}{{\text{s}}^{ - 2}} \\\$
The acceleration of the bigger body is found to be $2\,{\text{m}}{{\text{s}}^{ - 2}}$ .
Initial velocities of the two bodies are zero.
At time, $t = 5\,{\text{s}}$ , we have:
Final velocity of the smaller body becomes zero i.e.
${v_1} = 0\,{\text{m}}{{\text{s}}^{ - 1}}$
${v_2} = {u_2} + at$ …… (2)
Substituting the required values in equation (2), we get:
{v_2} = {u_2} + at \\\ {v_2} = 0 + 2 \times 5 \\\ {v_2} = 10\,{\text{m}}{{\text{s}}^{ - 1}} \\\
The final velocity of the bigger object is found out to be $10\,{\text{m}}{{\text{s}}^{ - 1}}$ .

This problem is truly based on the principle of conservation of linear momentum, that is we can alternatively say that momentum of the system is conserved before and after the collision.
Now, we apply the principle of conservation of linear momentum, which can be illustrated as follows:
$mv = {m_1}{v_1} + {m_2}{v_2}$ …… (3)
$m$ indicates mass of the combined system.
$v$ indicates velocity of the combined system.
${m_1}$ indicates mass of the first body.
${v_1}$ indicates velocity of the first body.
${m_2}$ indicates mass of the second body.
${v_2}$ indicates the velocity of the second body.
Substituting the required values in equation (1), we get:
mv = {m_1}{v_1} + {m_2}{v_2} \\\ \left( {2 + 3} \right) \times v = 2 \times 0 + 3 \times 10 \\\ 5v = 30 \\\ v = 6\,{\text{m}}{{\text{s}}^{ - 1}} \\\
Hence, the velocity of the combined system is found out to be $6\,{\text{m}}{{\text{s}}^{ - 1}}$ .

So, the correct answer is “Option C”.

Note:
In this problem, you will need the concept of conservation of linear momentum. It is important to note that, the sign convention gives us the direction of combined mass Since, velocity is a vector quantity, it will depend on direction too. Positive sign indicates that the bodies are moving in the same direction as assumed by us, while negative indicates that they are moving in the opposite direction in contrast to the direction assumed by us.