Question

Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite direction when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is:
A. 0
B. $\dfrac{2\pi }{3}$
C. $\pi$
D. $\dfrac{\pi }{6}$

Answer 1

As a first step, you could depict the given situation in a diagram. Then, you could write the equations for the displacement of the given two particles. Then find the angular displacement when the displacement is half the amplitude. Then you could take the difference of angular displacements of the two particles to get the required phase difference.

Complete Step by step solution:
In the question, we are given two particles that are oscillating side by side along two parallel straight lines with the same frequency and amplitudes. When their displacement is half their amplitudes, they are found to pass each other but moving in opposite directions to each other. We are also given that their mean positions lie on a straight line that is perpendicular to the paths of the two particles. We are supposed to find the phase difference between the two particles.

Let us first depict the given condition in a diagram.

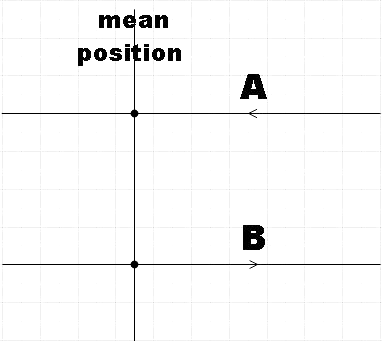
Let the displacement of the two particles 1 and 2 be given by,
${{y}_{1}}=A\sin \left( \omega t+{{\phi }_{1}} \right)$
${{y}_{2}}=A\sin \left( \omega t+{{\phi }_{2}} \right)$

We know that for a displacement of particle given by,$y=A\sin \left( \omega t+\phi \right)$, when the displacement is $\dfrac{A}{2}$,
$\dfrac{A}{2}=A\sin \left( \omega t+\phi \right)$
$\Rightarrow \sin \left( \omega t+\phi \right)=\dfrac{1}{2}$
$\Rightarrow \omega t+\phi ={{\sin }^{-1}}\left( \dfrac{1}{2} \right)$
$\therefore \left( \omega t+\phi \right)=\dfrac{\pi }{6},\dfrac{5\pi }{6}$

Therefore, we found the possible angular displacements of the particles to be $\dfrac{\pi }{6}$ and$\dfrac{5\pi }{6}$. From the figure, we see that angular displacement of the particle 1 is $\dfrac{5\pi }{6}$ and that of particle 2 would be$\dfrac{\pi }{6}$. That is,
$\left( \omega t+{{\phi }_{1}} \right)=\dfrac{5\pi }{6}$ ………………………………… (1)
$\left( \omega t+{{\phi }_{2}} \right)=\dfrac{\pi }{6}$………………………………… (2)

Subtracting equation (2) from equation (1), we get,
${{\phi }_{1}}-{{\phi }_{2}}=\dfrac{5\pi }{6}-\dfrac{\pi }{6}$
$\therefore {{\phi }_{1}}-{{\phi }_{2}}=\dfrac{4\pi }{6}=\dfrac{2\pi }{3}$

Therefore, we found the phase difference between the two given particles to be$\dfrac{2\pi }{3}$.

Hence, option B is found to be the correct answer.

Note:
We have written the above equations for the displacement of the given particles based on the given question that says that they both have the same frequency and amplitudes. The term $\phi$ in the equation of displacement is the respective phase angles of the particles. We could say that particle 1 moves to the extreme position before the other and passes each other on its way back.