Question

Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is?
(A) $0$
(B) $\dfrac{{2\pi }}{3}$
(C) $\pi$
(D) $\dfrac{\pi }{6}$

Answer 1

Here, you are given two particles which are oscillating along two different but close parallel straight lines, two conditions are given to you and you are asked to find out the phase difference between them. In order to find the phase difference, first you need to look for the definition of phase difference, after knowing what it is exactly, you go for the conditions given to you and then find the phase difference. Use the phase circle.

Complete step by step answer:
Let us look at what the phase difference is. Consider two particles oscillating along two close parallel straight lines. Let us denote the one particle or first particle by ${P_1}$ and the other particle or second particle as ${P_2}$. Let the mean positions, velocities, frequencies and the amplitude of oscillation be the same for both the particles. As far as the mean position is concerned, their y-coordinate differs by a small amount, but their x-coordinate is the same.

Let the mean position be $x = 0$. Let's say that at $t = 0$, the particle ${P_1}$ is at origin and ${P_2}$ is at maximum distance from the origin and their motion starts. You can see that the ${P_2}$ is enjoying its maximum distance from the origin but ${P_1}$ is not. Here, the phase difference is equal to $\dfrac{\pi }{2}$, because ${P_1}$ makes an angle of $\dfrac{\pi }{2}$ with the x-axis whereas ${P_2}$ makes an angle of $0$. So, phase difference can be understood as the difference in status enjoyed by each particle.

Let us come back to our question. There are two conditions given to you. First is that they have the same x-coordinate of mean position. Second is the positions and direction of velocities of the particles. ${P_1}$ is at $x = \dfrac{A}{2}$ moving in the positive x direction, ${P_2}$ is also at $x = \dfrac{A}{2}$ but moving in negative x direction. Now, we will find the phase difference between these particles using the phase circle as shown.

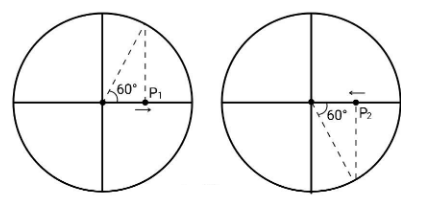
In the phase circle, the particles can be seen as projection of a particle which is performing circular motion in clockwise direction. The angle made by the line which connects the origin and the projection of particles on the circle can be used to find the phase difference. Basically, that angle tells you the state that a particular particle is enjoying. So, as you can see that the angle for ${P_1}$ is $60^\circ = \dfrac{\pi }{3}$, whereas the angle for ${P_2}$ is $- 60^\circ = - \dfrac{\pi }{3}$. So, the phase difference will be $\dfrac{\pi }{3} - \left( { - \dfrac{\pi }{3}} \right) = \dfrac{{2\pi }}{3}$. Therefore, the phase difference is $\dfrac{{2\pi }}{3}$.

Hence, option B is correct.

Note: We have discussed a method of finding the state possessed by a particle in motion and you are supposed to understand it and keep in mind. Also, you should be careful about the signs of the angles while measuring them. Keep in mind the orientation of the particle should always be either clockwise or anti-clockwise according to your convenience but stick with one orientation.