Question
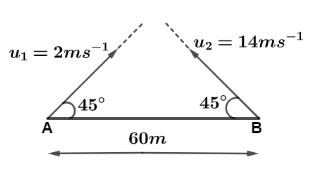
Question: Two particles are located on a horizontal plane at a distance of \(60\,m\) At \(t = 0\) both the par...
Two particles are located on a horizontal plane at a distance of 60m At t=0 both the particles are simultaneously projected at angle of 45∘ with velocity 2ms−1 and 14ms−1 respectively. Find
[a] Minimum separation between them during motion.
[b] At what time is the separation between them the minimum.
Solution
In order to solve the question we need to understand the definition of projectile motion which states that the path traced by a launched object under only force of gravitation and it continues its motion by virtue of its own inertia. Also relative motion is that motion than in which frame of reference has been fixed to one body and other body motion is analyzed.
Complete step by step answer:
[a] For minimum separation we need to analyze the motion of body A in respect of body B.According to the given question, the velocity of body A is v1=2ms−1 and v2=14ms−1. So velocity of body B with respect to body A is vBA=v2−v1. Adding according rule of vector addition we get vBA=(142)+(22) as angle between them is 90∘
The projectile diagram is shown as
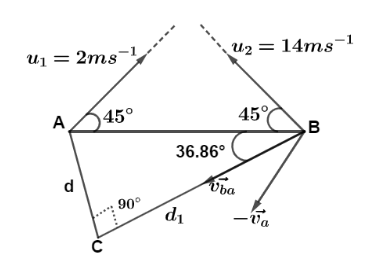
So vBA=14.142ms−1 and angle that it makes with vB is given by
tan(θ+45)=142
⇒θ+45=tan−1(142)=8.130
⇒θ=8.130−45=−36.86∘
Here negative sign implies that vBA is below the horizontal by 36.86∘
So we considered body A to be at rest then minimum separation between then is distance d
So d=60sin(36.86)
∴d=35.99m
So the minimum separation between them is 35.99m.
[b] For time we use that distance BC=d1=60cos(36.86)=48.0062m
So the time taken by particle to travel distance BC with speed vBA=14.142ms−1 and with 0 relative acceleration ( aBA=aB−aA=g−g=0 ) is t=vBAd1.
t=14.142msec−148.0062m ∴t=3.394s
So the minimum time required is 3.394s.
Note: It should be remembered that relative projectile motion would only be applied if one particle is considered at rest and only other moves. Here body A is considered to be at rest while B is moving but if reverse analysis done means B is at rest and A is moving the result would be the same. Also in relative projectile motion particles travel in a straight line.
