Question

Two particles A and B, move with constant velocities $\overrightarrow {{v_1}}$ and $\overrightarrow {{v_2}}$. At the initial moment their position vectors are $\overrightarrow {{r_1}}$ and $\overrightarrow {{r_2}}$ respectively. The condition for particles A and B for their collision is:
$\begin{aligned} &{\text{A}}{\text{. }}\overrightarrow {{r_1}} - \overrightarrow {{r_2}} = \overrightarrow {{v_1}} - \overrightarrow {{v_2}} \\\ &{\text{B}}{\text{. }}\dfrac{{\overrightarrow {{r_1}} - \overrightarrow {{r_2}} }}{{|\overrightarrow {{r_1}} - \overrightarrow {{r_2}} |}} = \dfrac{{\overrightarrow {{v_2}} - \overrightarrow {{v_1}} }}{{|\overrightarrow {{v_2}} - \overrightarrow {{v_1}} |}} \\\ &{\text{C}}{\text{. }}\overrightarrow {{r_1}} .\overrightarrow {{v_1}} = \overrightarrow {{r_2}} .\overrightarrow {{v_2}} \\\ &{\text{D}}{\text{. }}\overrightarrow {{r_1}} \times \overrightarrow {{v_1}} = \overrightarrow {{r_2}} \times \overrightarrow {{v_2}} \\\ \end{aligned}$

Answer 1

For the collision to take place between the particle A and B, the relative position of one particle with respect to another should have the direction the same as the relative position of the second particle with respect to the first. The relative velocities of the two particles should also have the same directions. Equating the expressions of relative positions and the relative velocities, we can obtain the required answer.

Complete step-by-step solution:
We are given two particles A and B which are moving with constant velocities and their velocity vectors are given as $\overrightarrow {{v_1}}$ and $\overrightarrow {{v_2}}$ respectively. The position vectors of the two particles are given as $\overrightarrow {{r_1}}$ and $\overrightarrow {{r_2}}$ respectively.
Now we need to find the condition for particles A and B such that their collision takes place.
We can find this condition on the basis of the fact that the relative positions and the relative velocities should have the same direction.

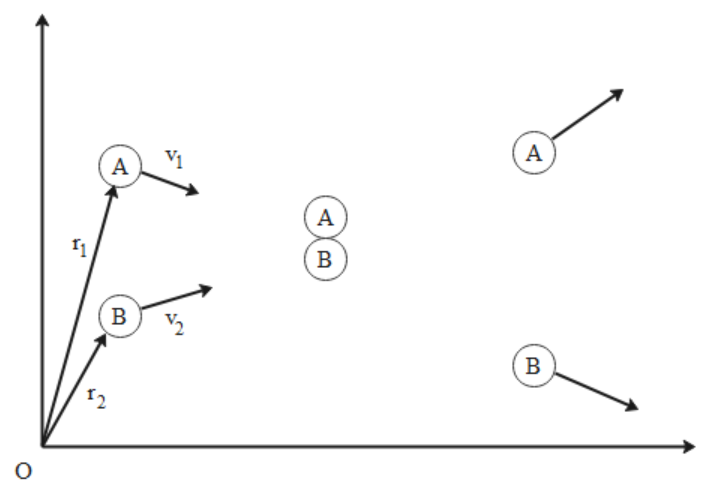
The relative position of particle A with respect to particle B is given as
$\dfrac{{\overrightarrow {{r_1}} - \overrightarrow {{r_2}} }}{{|\overrightarrow {{r_1}} - \overrightarrow {{r_2}} |}}$
Similarly, the relative velocity of particle A with respect to particle B is given as
$\dfrac{{\overrightarrow {{v_2}} - \overrightarrow {{v_1}} }}{{|\overrightarrow {{v_2}} - \overrightarrow {{v_1}} |}}$
Now these two vectors must have same direction in order for the particle to collide. Therefore, we can write the following expression.
$\dfrac{{\overrightarrow {{r_1}} - \overrightarrow {{r_2}} }}{{|\overrightarrow {{r_1}} - \overrightarrow {{r_2}} |}} = \dfrac{{\overrightarrow {{v_2}} - \overrightarrow {{v_1}} }}{{|\overrightarrow {{v_2}} - \overrightarrow {{v_1}} |}}$
This is the required expression for the condition that particle A collides with particle B. Hence, the correct answer is option B.

Note: 1. The condition for collision means that they are directed towards the same point in space which ensures that eventually the particles will meet and collide at that point of space.
2. The expressions in the condition represent a unit vector since we have divided the vector by its magnitude. The purpose of a unit vector is to give direction only.