Question

Two particles A and B having charges $q$ and $2q$ respectively are placed on a smooth table with a separation of $d$ . A third particle is C is to be clamped on the table in such a way that the particle A and B remain at rest on the table under electrical forces. What should be the charge on C and where should it be clamped?

Answer 1

Here, the question says that the two charges are placed on the table and the third particles is clamped such that the two charges remain at rest so we have to balance the forces acting on them such that the particle C should be placed in between of the two particles A and B. Use the concept of electrostatic force acting on a particle due to another particle.

Complete step by step answer:
Let the particle C have charge $Q$ and also let the particle C be lying between the two particles on the table A and B (assumption). As shown in the figure below:

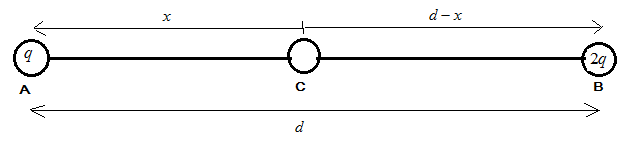
In the above figure:
$d$ is the distance between the charges at A and B.
$x$ is the distance between A and C, C is between A and B.
$d - x$ is the distance between C and B.
$q$, $2q$, $Q$ are the charges on the particles A, B and C respectively.
Now, we have to use the concept of balancing forces such that
${F_{AC}} = {F_{BC}}$ ….( ${F_{AC}}$ is the force between A and C ${F_{BC}}$ is the force between B and C)
${F_{AC}} = \dfrac{{kqQ}}{{{x^2}}}$ and ${F_{BC}} = \dfrac{{k(2q)Q}}{{{{(d - x)}^2}}}$
Using these value in above equation we get,
$\Rightarrow \dfrac{{kqQ}}{{{x^2}}} = \dfrac{{k(2q)Q}}{{{{(d - x)}^2}}}$
$\Rightarrow \dfrac{{{k}{q}{Q}}}{{{x^2}}} = \dfrac{{{k}(2{q}){Q}}}{{{{(d - x)}^2}}}$
$\Rightarrow \dfrac{1}{x} = \dfrac{{\sqrt 2 }}{{d - x}}$ $\Rightarrow x = d(\sqrt 2 - 1)$ ….. $(1)$
Now, the forces $\overrightarrow {{F_{AC}}}$ and $\overrightarrow {{F_{AB}}}$ are in opposite directions so that the particles remain at rest.
$\therefore$ $\overrightarrow {{F_{AC}}} + \overrightarrow {{F_{AB}}} = 0$
$\Rightarrow \dfrac{{kqQ}}{{{x^2}}} = - \dfrac{{k(2q)q}}{{{d^2}}}$
$\Rightarrow \dfrac{{{k}{q}Q}}{{{x^2}}} = - \dfrac{{{k}(2q){q}}}{{{d^2}}}$
$\Rightarrow Q = - \dfrac{{{x^2}}}{{{d^2}}} \times 2q = - \dfrac{{{d^2}{{(\sqrt 2 - 1)}^2}}}{{{d^2}}} \times 2q$ ….. (from $(1)$ )
$\Rightarrow Q = - (2 + 1 - 2\sqrt 3 )2q$
$\Rightarrow Q = - (6 - 4\sqrt 3 )q$
Thus, the charge on particle C is $(6 - 4\sqrt 3 )q$ and it is negative because if it's positive the other charges will be repelled and would not be at rest. So to keep those at rest C must be negative.

Note:
The forces here are balanced by us as the question clearly says that the particles should be at rest and the particle is kept between the particles A and B such that these particles will not get displaced. The particle C possesses the negative charge to balance the forces between all the three charges.