Solveeit Logo
Login

Question

Question: Two particles A and B having charges of \[4 \times {10^{ - 6}}C\] and \[ - 64 \times {10^{ -6}}C\] r...

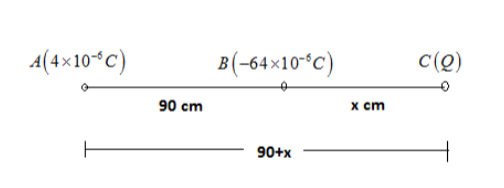
Two particles A and B having charges of 4×10−6C4 \times {10^{ - 6}}C and −64×10−6C - 64 \times {10^{ -6}}C respectively are held at a separation of 90 cm. Locate the point(s) on the line AB or on its extension where the electric field is zero.

Explanation

Solution

We know the electric field between the two point is given by the formula F=kQqr2F = k\dfrac{{Qq}}{{{r^2}}}, where Q and q is the charge on the particles and r is the distance between them, in this question two points charges are given and we will assume a third charge on the line AB and then we will find the electric field on point charge C from the point A and the point B. And the we will find that point C.

Complete step by step answer:
Charge on particle A =4×10−6C = 4 \times {10^{ - 6}}C
Charge on particle B =−64×10−6C = - 64 \times {10^{ - 6}}C
Separation between the two particles A and B d=90cm=90100=0.9md = 90cm = \dfrac{{90}}{{100}} = 0.9m
Now let us assume the charger on the particle C to be Q which lie to the right of point B on the line AB where the electric field will be equal to zero

We know the amount of force between the two stationary and electric charged particles is defined by coulomb law which is given by the formula as
F=kQqr2F = k\dfrac{{Qq}}{{{r^2}}}
So the electric field between the particle A and C which is at distance (90+x) cm will be equal to
FAC=kQ(4×10−6)(0.9+x)2−−(i){F_{AC}} = k\dfrac{{Q\left( {4 \times {{10}^{ - 6}}} \right)}}{{{{\left( {0.9 + x} \right)}^2}}} - - (i)
And the electric field between the particle B and C which is at distance x cm will be equal to
FBC=kQ(−64×10−6)(x)2−−(ii){F_{BC}} = k\dfrac{{Q\left( { - 64 \times {{10}^{ - 6}}} \right)}}{{{{\left( x \right)}^2}}} - - (ii)
Now equate equation (i) with equation (ii) to find the distance x where the electric field is zero
kQ(4×10−6)(0.9+x)2=kQ(−64×10−6)(x)2k\dfrac{{Q\left( {4 \times {{10}^{ - 6}}} \right)}}{{{{\left( {0.9 + x} \right)}^2}}} = k\dfrac{{Q\left( { - 64 \times {{10}^{ - 6}}} \right)}}{{{{\left( x \right)}^2}}}
By further solving we get

(4×10−6)(0.9+x)2=(−64×10−6)(x)2 ⇒(x)2(4×10−6)=(0.9+x)2(−64×10−6) ⇒x2=(x2+0.81+1.8x)(−16) ⇒x2=−16x2−28.8x−12.96 ⇒17x2+28.8x+12.96=0  \dfrac{{\left( {4 \times {{10}^{ - 6}}} \right)}}{{{{\left( {0.9 + x} \right)}^2}}} = \dfrac{{\left( { - 64 \times {{10}^{ - 6}}} \right)}}{{{{\left( x \right)}^2}}} \\\ \Rightarrow {\left( x \right)^2}\left( {4 \times {{10}^{ - 6}}} \right) = {\left( {0.9 + x} \right)^2}\left( { - 64 \times {{10}^{ - 6}}} \right) \\\ \Rightarrow {x^2} = \left( {{x^2} + 0.81 + 1.8x} \right)\left( { - 16} \right) \\\ \Rightarrow {x^2} = - 16{x^2} - 28.8x - 12.96 \\\ \Rightarrow 17{x^2} + 28.8x + 12.96 = 0 \\\

So we get the distance x in the quadratic form
17x2+28.8x+12.96=017{x^2} + 28.8x + 12.96 = 0
So by solving the roots of the quadratic equation we get
x=−28.8±(28.8)2−4(17)(12.96)2(17) ⇒x=−28.8±829.44−881.2834 ⇒x=−28.8±−51.8434 ⇒x=−28.8±i7.234  x = \dfrac{{ - 28.8 \pm \sqrt {{{\left( {28.8} \right)}^2} - 4(17)(12.96)} }}{{2(17)}} \\\ \Rightarrow x = \dfrac{{ - 28.8 \pm \sqrt {829.44 - 881.28} }}{{34}} \\\ \Rightarrow x = \dfrac{{ - 28.8 \pm \sqrt { - 51.84} }}{{34}} \\\ \Rightarrow x = \dfrac{{ - 28.8 \pm i7.2}}{{34}} \\\

Hence, the point(s) on the line AB or on its extension where the electric field is zero are −28.8+i7.234\dfrac{{ - 28.8 + i7.2}}{{34}} and −28.8−i7.234\dfrac{{ - 28.8 - i7.2}}{{34}}.

Note: Here, the points are lying on the coordinates axes where the terms associated with the imaginary terms indicates the distance of the point on the y-axis from the origin and the real terms indicates the distance of the point on the x-axis from the origin.