Question

Two particles $A$ and $B$ are projected simultaneously from ground towards each other as shown. If they collide in mid-air then, the height above the ground where they collide is:

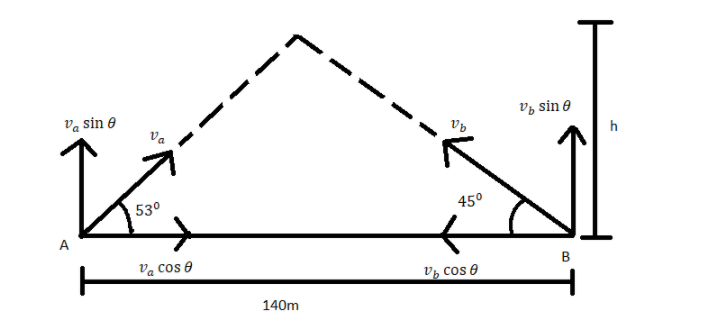
(A) $75m$
(B) $25m$
(C) $100m$
(D) $125m$

Answer 1

We will solve this question with the help of basic equations of projectile motion and relative motion. Projectile motion is a form of motion experienced by an object or particle that is projected near the Earth's surface and moves along a curved path under the action of gravity only.
Formula Used:
The formula for height of the particle at any time $t$ sec:
$h = ut + \dfrac{1}{2}a{t^2}$
Where
$t$ is time in seconds
$h$ is height of the particle at any point of time
$u$ is the initial speed of the particle
$a$ is the acceleration due to gravity

Complete Step-by-Step Solution:
Let us suppose that both the particles meet at a height $h$ from ground level.
Then in X-axis,
Distance between both the particles is $140m$
${v_a}$ in X-axis $= 100\cos {53^\circ }$
$= 100 \times \dfrac{3}{5} = 60m/s$
The relative velocity between the two particles is given by
${v_{ab}} = {v_a} - {v_b}$
$\Rightarrow {v_{ab}} = 60 - ( - \dfrac{{{v_b}}}{{\sqrt 2 }})$
Hence we get,
$\Rightarrow {v_{ab}} = 60 + \dfrac{{{v_b}}}{{\sqrt 2 }}$
So, the time of collision, $t = \dfrac{{140}}{{60 + \dfrac{{{v_b}}}{{\sqrt 2 }}}}$
In Y-axis
Height at which they collide is same as $h$
$h = {v_a}\sin {53^\circ } - \dfrac{1}{2}g{t^2}$ …………………. (i)
Also,
$h = {v_b}\sin {45^\circ } - \dfrac{1}{2}g{t^2}$ …………………(ii)
$\Rightarrow 100\sin {53^\circ } + ( - \dfrac{1}{2} \times 10 \times {t^2}) = {v_b}\sin 45 \times t - \dfrac{1}{2}g{t^2}$
Hence we get,
$\Rightarrow 100 \times \dfrac{4}{5} = \dfrac{{{v_b}}}{{\sqrt 2 }}$
$\therefore {v_b} = 80\sqrt 2 m/s$
Time of collision $= \dfrac{{140}}{{60 + \dfrac{{80\sqrt 2 }}{{\sqrt 2 }}}}$ $= 1\sec$
Now we put the values of $t$ in equation (i), we get
$h = 80 + ( - \dfrac{1}{2} \times 10 \times {t^2})$
$\Rightarrow h = 80 \times 1 - \dfrac{1}{2} \times 10 \times {1^2}$
Therefore we get,
$\therefore h = 75cm$
Now we will conform our answer by putting the value in equation (ii)
$\Rightarrow h = 80\sqrt 2 \times \dfrac{1}{{\sqrt 2 }} \times 1 - \dfrac{1}{2} \times 10 \times {1^2}$
$\Rightarrow h = 80 - 5 = 75m$

Hence the correct answer is option A.

Note: We should always confirm the answer by putting the value of $t$ in the equation (i) and (ii) obtained. This will correct our errors in case we have accidently made and our final answer will be more accurate.