Question

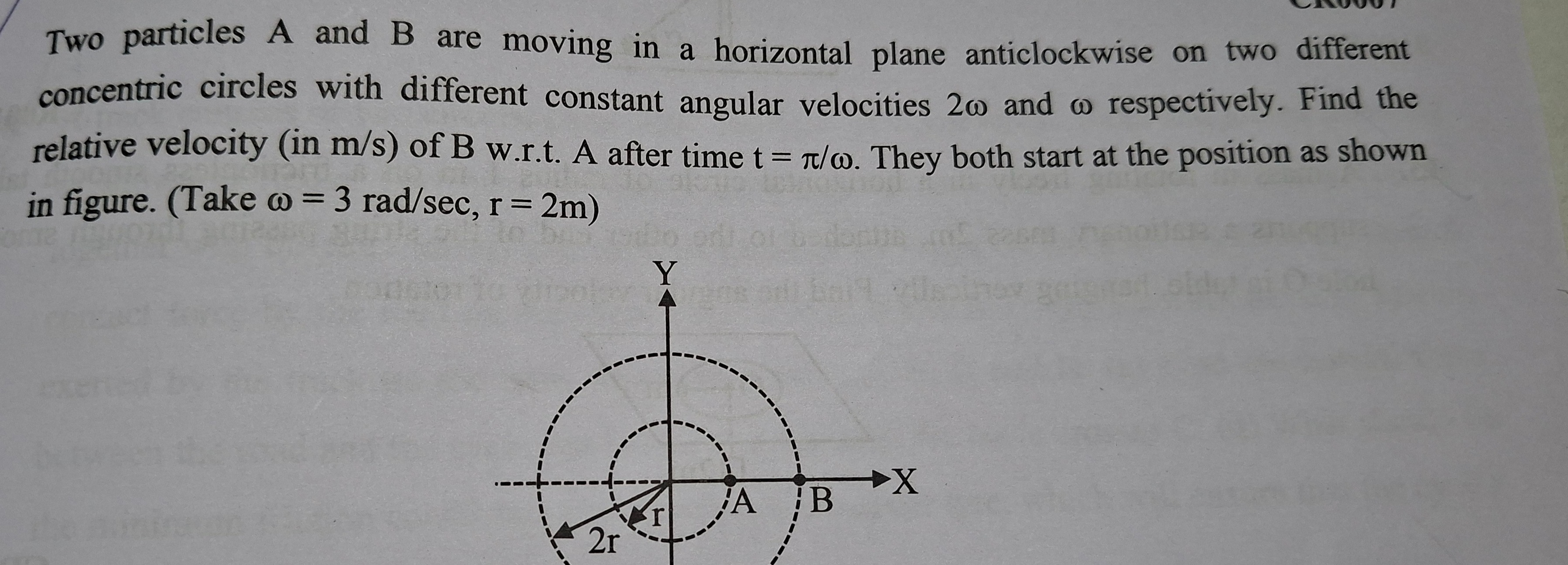
Two particles A and B are moving in a horizontal plane anticlockwise on two different concentric circles with different constant angular velocities $2\omega$ and $\omega$ respectively. Find the relative velocity (in m/s) of B w.r.t. A after time $t = \pi/\omega$. They both start at the position as shown in figure. (Take $\omega$ = 3 rad/sec, r = 2m)

• A. 24 m/s
• B. 12 m/s
• C. 36 m/s
• D. 0 m/s

Answer 1

Answer: (A)

24 m/s

Answer 2

1. Initial Conditions:

   • Particle A: Radius $R_A = r$, initial position on positive x-axis.
   • Particle B: Radius $R_B = 2r$, initial position on positive x-axis.
   • Angular velocities: $\omega_A = 2\omega$ (anticlockwise), $\omega_B = \omega$ (anticlockwise).
   • Time $t = \pi/\omega$.
   • Given values: $\omega = 3$ rad/sec, $r = 2$ m.

2. Angular Positions at time $t = \pi/\omega$:

   • For particle A: $\theta_A(t) = \theta_A(0) + \omega_A t = 0 + (2\omega)(\pi/\omega) = 2\pi$.
   • For particle B: $\theta_B(t) = \theta_B(0) + \omega_B t = 0 + (\omega)(\pi/\omega) = \pi$.

3. Velocities at time $t = \pi/\omega$: The velocity vector for a particle in anticlockwise circular motion starting from the positive x-axis is given by $\vec{v} = R\omega(-\sin\theta \hat{i} + \cos\theta \hat{j})$.

   • For particle A:
     • $\theta_A = 2\pi$
     • $\vec{v}_A = R_A \omega_A (-\sin(2\pi) \hat{i} + \cos(2\pi) \hat{j}) = r(2\omega)(0\hat{i} + 1\hat{j}) = 2r\omega \hat{j}$.
   • For particle B:
     • $\theta_B = \pi$
     • $\vec{v}_B = R_B \omega_B (-\sin(\pi) \hat{i} + \cos(\pi) \hat{j}) = (2r)(\omega)(0\hat{i} - 1\hat{j}) = -2r\omega \hat{j}$.

4. Relative Velocity of B with respect to A: $\vec{v}_{B/A} = \vec{v}_B - \vec{v}_A$ $\vec{v}_{B/A} = (-2r\omega \hat{j}) - (2r\omega \hat{j}) = -4r\omega \hat{j}$.

5. Magnitude of Relative Velocity: Substitute the given values: $r = 2$ m, $\omega = 3$ rad/sec. $|\vec{v}_{B/A}| = |-4 \times (2 \text{ m}) \times (3 \text{ rad/sec}) \hat{j}| = |-24 \hat{j}| \text{ m/s} = 24 \text{ m/s}$.