Question

Two particles $1$ and $2$ move with constant velocities ${v_1}$ and ${v_2}$ . At the initial moment their radius vectors are equal to ${r_1}$ and ${r_2}$ . The relation between four vectors for the particles to collide is $\dfrac{{({{\vec r}_1} - {{\vec r}_2})}}{{\left| {{{\vec r}_1} - {{\vec r}_2}} \right|}} = x\dfrac{{({{\vec v}_1} - {{\vec v}_2})}}{{\left| {{{\vec v}_1} - {{\vec v}_2}} \right|}}$. Find $x$.

Answer 1

In order to solve this question we need to understand the rule of vector addition. First defining vectors, so vectors are scalar having a particular direction. So in order to add two vectors with direction we use a method known as triangle rule of vector addition and later to add more vectors we use polygonal law of vector addition. Triangle law of vector addition states that if we add two vectors such that they form two sides of a triangle then the third side represents a vector which is the sum of two vectors.

Complete step by step answer:
Let the first particle be at point A and second particle be at point B
Let the position vector of first particle be OA and it is equal to ${\vec r_1}$
And second position vector of second particle be OB and it is equal to ${\vec r_2}$

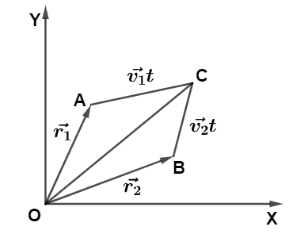
Let the first particle start moving towards second with speed ${\vec v_1}$ and second particle starts moving towards first with ${\vec v_2}$ .Let these particles collide with each other at $C$. Also let time “t” be taken to move each particle from their respective positions to $C$.Then from triangle law of vector addition in triangle $\Delta OAC$ we have $O\vec C = O\vec A + A\vec C$.

That is $O\vec C = {\vec r_1} + {\vec v_1}t$. Similarly in the triangle $\Delta OBC$ we have $O\vec C = O\vec B + B\vec C$. That is $O\vec C = {\vec r_2} + {\vec v_2}t$.
Equating both $O\vec C$ we get ${\vec r_1} + {\vec v_1}t = {\vec r_2} + {\vec v_2}t$.
$({\vec r_1} - {\vec r_2}) = t({\vec v_1} - {\vec v_2})$
Since time is scalar so
$t = \dfrac{{\left| {{{\vec r}_1} - {{\vec r}_2}} \right|}}{{\left| {{{\vec v}_1} - {{\vec v}_2}} \right|}}$
So putting value of t we get
$\dfrac{{({{\vec r}_1} - {{\vec r}_2})}}{{\left| {{{\vec r}_1} - {{\vec r}_2}} \right|}} = \dfrac{{({{\vec v}_1} - {{\vec v}_2})}}{{\left| {{{\vec v}_1} - {{\vec v}_2}} \right|}}$
Comparing with problem given we get $x = 1$

Hence the correct answer is $x = 1$.

Note: It should be remembered that here we do not concern with direction of final vector also here collision type not considered whether elastic or in-elastic collision. In elastic collision both momentum and energy is conserved but in in-elastic collision only momentum is conserved because energy is lost by mechanical force in performing work either for or against the motion.