Question
Question: Two particles 1 and 2 are allowed to descend on two frictionless chords \[OP\] and \[OQ\] . The rati...
Two particles 1 and 2 are allowed to descend on two frictionless chords OP and OQ . The ratio of the speeds of the particles 1 and 2 respectively when they reach on the circumference is:
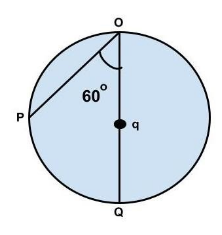
A. 41
B. 21
C. 1
D. 221
Solution
Before going through the question let us first talk about work. In physics, work is energy transferred through the use of force throughout a displacement to or from an object. It is often depicted as a product of strength and displacement in its simplest form.
Complete step by step answer:
Let the radius of the given circle = R
Oq=Pq=R ΔOPq
So, ΔOPq is an equilateral triangle.
So Particle on chord OP will travel vertical distance = Rcos60=2R
Work is closely connected with energy. The principle of work-energy says that increasing the kinetic energy of a rigid body is caused by equal amounts of positive work done on the body by the consequent power acting on it.
On the other hand, an equal amount of negative work done by the resulting force is caused to reduce the kinetic energy. So, if the network is good, the kinetic energy of the particle increases by the quantity of work. When the network is negative, the film energy of the particle decreases by the quantity of the work. Therefore, from work-energy theorem :
mg(2R)=21mv12 ⇒v1=Rg
Particle on the chord OQ will travel a vertical distance = 2R
Similarly for particle on OQ :
v2=4Rg=2Rg
Therefore ratio of their speed is : v2v1=21
Hence, the ratio of the speeds of the particles 1 and 2 respectively when they reach the circumference is: 21.
Note: If you are aware of the motion of an object but are not familiar with the values of one or more of the forces acting on it, you can use the work-energy theorem to gain some information about these forces.
