Question

Two parallel wires in the place of the paper are distance ${X_0}$ apart. A point charge is moving with speed $u$ between the wires in the same plane at a distance ${X_1}$ from one of the wires. When the wires carry current of magnitude $I$ in the same direction, the radius of curvature of the path of the point charge is ${R_1}$ . In contrast, if the current has opposite directions to each other, the radius of the curvature of the path is ${R_2}$ . If $\dfrac{{{X_0}}}{{{X_1}}} = 3$ , the value of $\dfrac{{{R_1}}}{{{R_2}}}$ is
(A) 3
(B) 7
(C) 2
(D) 5

Answer 1

Hint : For current in the same direction, find the difference between the magnetic fields at the charge while for currents in opposite directions, add the magnetic fields. And the radius of curvature is inversely proportional to the magnetic field.

Formula used: $B = \dfrac{{{\mu _0}I}}{{2\pi x}}$ where $B$ is the magnetic field, ${\mu _0}$ is the permeability of free space and $x$ is the distance from the wire.

Complete step by step answer

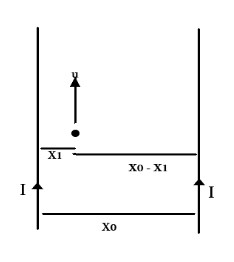
The field experienced by the charge due to the wire on its left (say wire 1) is given as
$\Rightarrow {B_1} = \dfrac{{{\mu _0}I}}{{2\pi {x_1}}}$
And the field experienced by the charge due to the wire on its right (say wire 2) is given as
$\Rightarrow {B_2} = \dfrac{{{\mu _0}I}}{{2\pi ({x_0} - {x_1})}}$
The total field experienced by the charge when the current are in the same direction is given by subtracting the magnetic fields as in
$\Rightarrow B_{1,2}^ - = \dfrac{{{\mu _0}I}}{{2\pi {x_1}}} - \dfrac{{{\mu _0}I}}{{2\pi ({x_0} - {x_1})}}$
This is because the field points in the different direction at location of charge.
Factoring $\dfrac{{{\mu _0}I}}{{2\pi }}$ out, we get
$\Rightarrow B_{1,2}^ - = \dfrac{{{\mu _0}I}}{{2\pi }}\left( {\dfrac{1}{{{x_1}}} - \dfrac{1}{{{x_0} - {x_1}}}} \right) \\\ \Rightarrow B_{1,2}^ - = \dfrac{{{\mu _0}I}}{{2\pi }}\left[ {\dfrac{{({x_0} - {x_1}) - {x_1}}}{{{x_1}({x_0} - {x_1})}}} \right] \\\$
Thus, by subtraction in the numerator we get,
$\Rightarrow B_{1,2}^ - = \dfrac{{{\mu _0}I}}{{2\pi }}\left( {\dfrac{{{x_0} - 2{x_1}}}{{{x_1}({x_0} - {x_1})}}} \right)$
For the current in the opposite direction, we add magnetic fields.
$\Rightarrow B_{1,2}^ + = \dfrac{{{\mu _0}I}}{{2\pi {x_1}}} + \dfrac{{{\mu _0}I}}{{2\pi ({x_0} - {x_1})}}$
Similarly, by factorization and addition, we get
$\Rightarrow B_{1,2}^ - = \dfrac{{{\mu _0}I}}{{2\pi }}\left[ {\dfrac{{{x_0}}}{{{x_1}({x_0} - {x_1})}}} \right]$
The radius of curvature of a charge in a magnetic field is inversely related to the magnetic field $B$ i.e.
$\Rightarrow R \propto \dfrac{1}{B} \\\ \Rightarrow R = \dfrac{k}{B} \\\$
Where $k$ is a constant. Thus,
$\Rightarrow RB = k \\\ \Rightarrow {R_1}B_{1,2}^ - = {R_2}B_{1,2}^ + \\\$
Then, dividing both sides by ${R_2}$ and $B_{1,2}^ -$ ,
$\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{B_{1,2}^ + }}{{B_{1,2}^ - }}$
Therefore, inserting the expressions for $B_{1,2}^ +$ and $B_{1,2}^ -$ in equation above, we have
\Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{\mu _0}I}}{{2\pi }}\left[ {\dfrac{{{x_0}}}{{{x_1}({x_0} - {x_1})}}} \right] \div \left\\{ {\dfrac{{{\mu _0}I}}{{2\pi }}\left[ {\dfrac{{{x_0} - 2{x_1}}}{{{x_1}({x_0} - {x_1})}}} \right]} \right\\}\, \\\ \Rightarrow \dfrac{{{\mu _0}I}}{{2\pi }}\left[ {\dfrac{{{x_0}}}{{{x_1}({x_0} - {x_1})}}} \right] \times \dfrac{{2\pi }}{{{\mu _0}I}}\left[ {\dfrac{{{x_1}({x_0} - {x_1})}}{{{x_0} - 2{x_1}}}} \right] \\\
Eliminating ${\mu _0}I$ , $2\pi$ and ${x_1}({x_0} - {x_1})$ we get
$\Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{x_0}}}{{{x_0} - 2{x_1}}}$
Dividing numerator and denominator by ${x_1}$ we get,
$\Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{\dfrac{{{x_0}}}{{{x_1}}}}}{{\dfrac{{{x_0}}}{{{x_1}}} - 2}} = \dfrac{3}{{3 - 2}} = 3$ (since $\dfrac{{{x_0}}}{{{x_1}}} = 3$ )
Hence, the correct option is A.

Note
In the calculation of the total magnetic field, we subtracted when the current are facing the same direction because using the right hand rule (which states that if your thumb points in the direction of the current, then your fingers curl around the direction of the magnetic field), the magnetic field due to wire 1 points into the page but the magnetic field due to wire two points out of the page. However, when they are in opposite directions the magnetic fields of wire 1 and 2 both point out of the page.