Question

Two parallel wires carrying equal currents in opposite directions are placed at $x=\pm a$ parallel to y-axis with $z=0$. Magnetic field at origin $O$ is ${{B}_{1}}$and at $P(2a,0,0)$ is ${{B}_{2}}$. Then the ratio $\dfrac{{{B}_{1}}}{{{B}_{2}}}$ is
$\text{A}\text{. }3$
$\text{B}\text{. }\dfrac{1}{2}$
$\text{C}\text{. }\dfrac{1}{3}$
$\text{D}\text{. }2$

Answer 1

Hint: We will calculate the value of the magnetic field at origin and point P due to each wire individually. For determining the direction of magnetic field lines, we will use the right hand thumb rule. The ratio of the resultants of the magnetic field at origin O and point P will be the required answer.

Formula used:
Magnetic field due to straight current carrying conductor, $B=\dfrac{{{\mu }_{o}}I}{2\pi r}$

Complete step by step answer:
Magnetic field due to a straight current carrying conductor is given by,
$B=\dfrac{{{\mu }_{o}}I}{2\pi r}$
Where,
$I$ is the current flowing through the conductor
$r$ is the distance of point from the wire
Magnetic field due to a straight current carrying conductor depends upon:
1. Current in the conductor. The value of the magnetic field is directly proportional to the amount of current flowing through the wire.
That is, $B\propto I$
2. Distance from the wire. The value of the magnetic field at a point is inversely proportional to the distance of point from the wire.
That is, $B\propto \dfrac{1}{r}$

Magnetic field lines around a straight current conductor are concentric loops whose centers lie on the wire length. The direction of the magnetic field is determined using Right-hand thumb rule. According to the right hand thumb rule, imagine that you are holding a current carrying straight wire in your right hand so that the thumb points in the direction of current, then the direction in which the fingers wrap the wire will represent the direction of magnetic lines of force.

Let the wire on right hand side (RHS) at $x=a$ carries current in vertically upward direction and wire on the left hand side (LHS) at $x=-a$ carries current in vertically downward direction. Consider RHS wire as a current carrying conductor placed in a magnetic field due to LHS wire. Similarly, LHS wire is a current carrying conductor kept in a magnetic field due to RHS wire. Both the wires will experience some amount of force. Magnetic field vectors in both LHS and RHS wires will be out of plane.

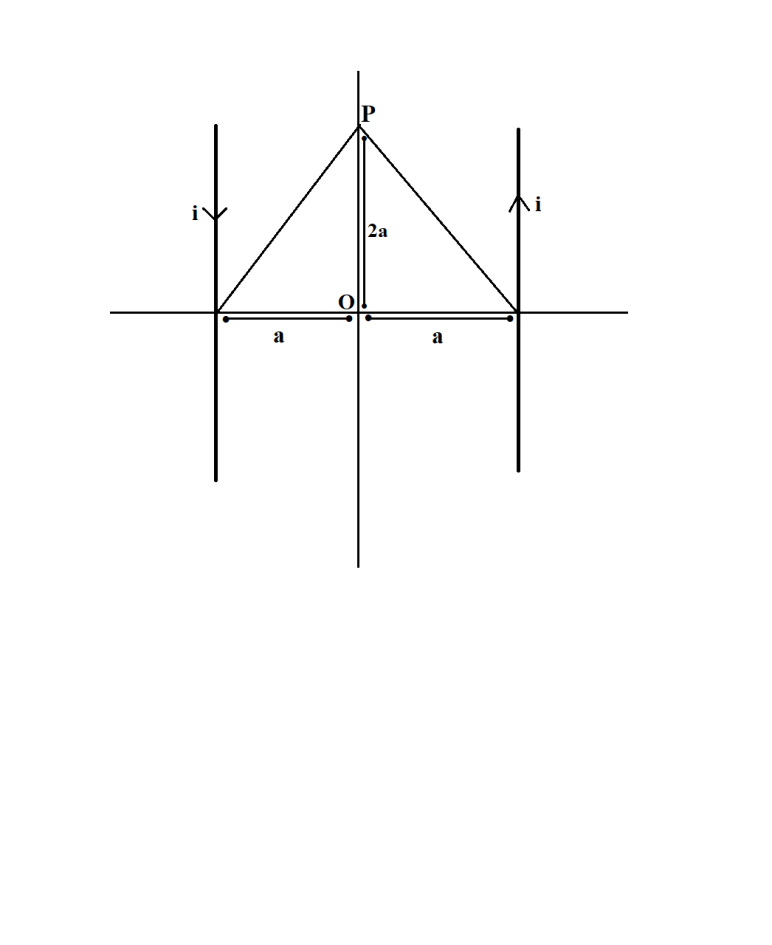
Magnetic field due to a current carrying conductor (straight wire) having current $I$ at a distance $x=r$ from the wire is given by:
$B=\dfrac{{{\mu }_{o}}I}{2\pi r}$
Calculating magnetic field at origin$\text{O}$,
$\begin{aligned} & {{B}_{1}}=-2\left( \dfrac{{{\mu }_{o}}}{2\pi }\dfrac{i}{a} \right)\widehat{k} \\\ & {{B}_{1}}=-\dfrac{{{\mu }_{o}}i}{\pi a}\widehat{k} \\\ \end{aligned}$
Magnetic field at point $P(2a,0,0)$
$\begin{aligned} & {{B}_{2}}=\dfrac{{{\mu }_{o}}}{2\pi }\dfrac{i}{a}\widehat{k}-\dfrac{{{\mu }_{o}}}{2\pi }\dfrac{i}{3a}\widehat{k} \\\ & {{B}_{2}}=\dfrac{{{\mu }_{o}}}{3\pi }\dfrac{i}{a}\widehat{k} \\\ \end{aligned}$
Ratio of ${{B}_{1}}$and ${{B}_{2}}$
$\dfrac{{{B}_{1}}}{{{B}_{2}}}=\dfrac{-\dfrac{{{\mu }_{o}}}{\pi }\dfrac{i}{a}\widehat{k}}{\dfrac{{{\mu }_{o}}}{3\pi }\dfrac{i}{a}\widehat{k}}=3$
$\dfrac{{{B}_{1}}}{{{B}_{2}}}=3$
Hence, the correct option is A.

Note: While calculating the value of the magnetic field, always remember to use the Right-hand thumb rule. According to the direction of the magnetic field, resultant magnetic field at a point can vary. Be careful while performing the calculations.