Solveeit Logo
Login

Question

Question: Two parallel plate capacitors of capacitance \( C \) and \( 2C \) are connected in parallel and char...

Two parallel plate capacitors of capacitance CC and 2C2C are connected in parallel and charged to a potential difference VV .If the battery is connected and the space between the plate of the capacitor of capacitance CC is completely filled with a material of dielectric constant kk , then the potential across the capacitor will be :

Explanation

Solution

Hint : Here, Capacitors are the components in the electric circuit which stores charge according to the capacity of the capacitor. The combinatorial formula for calculating the capacitance of capacitors connected in parallel is similar to that of the resistance equivalent we calculate in series. And vice versa. Use the proper circuit diagram according to the conditions given in the question.

Complete Step By Step Answer:
According to the condition given in the question let us draw a proper circuit diagram containing two capacitors in the parallel combination and a potential is applied to them as shown in the figure (1)(1)

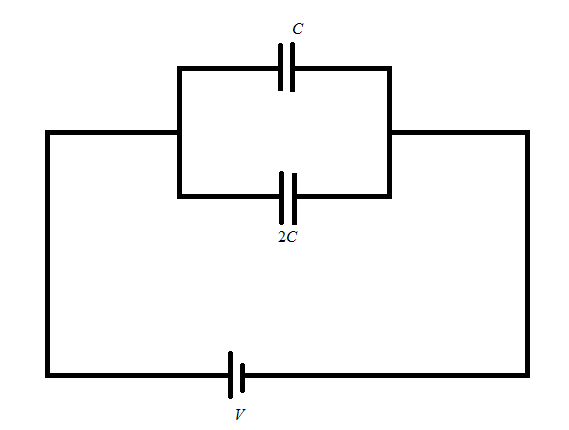
First, let the charge on capacitor CC be q1=CV{q_1} = CV
And charge on capacitor 2C2C be q2=2CV{q_2} = 2CV
Also, it is given that the capacitor with capacitance CC is filled with dielectric kk and V′V' be the potential through both the capacitors such that as shown in the figure (2)(2)

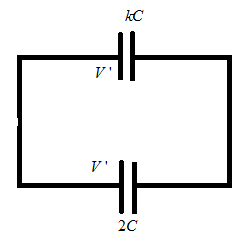
Now, when dielectric is filled in capacitor CC the charge becomes q1′=kCV′{q_1}' = kCV'
And similarly for capacitor 2C2C charge becomes q2′=2CV′{q_2}' = 2CV'
From figures (1)(1) and (2)(2) , we know that the total charge will remain conserved
That is why, we have to use the formula for conservation of charges in capacitors having same capacitance but different voltage across them to calculate new potential difference.
∴CV+2CV=kCV′+2CV′\therefore CV + 2CV = kCV' + 2CV'
∴V′=3Vk+2\therefore V' = \dfrac{{3V}}{{k + 2}}
The new voltage across the capacitor CC is V′=3Vk+2V' = \dfrac{{3V}}{{k + 2}} .

Note :
We know that the definition says that the charges on a capacitor is the product of the capacity of the capacitor and the potential difference across it i.e. q=CVq = CV . We have used this formula to find the potential difference when the dielectric is added.