Question

Two parallel plane mirrors ${M_1}$and ${M_2}$ have a length of $2m$ each and are $20mm$ apart. A ray of light is incident on one end of the mirror ${M_2}$ at an angle ${30^ \circ }$. The number of reflection, the light ray undergoes before it reaches the other one would be

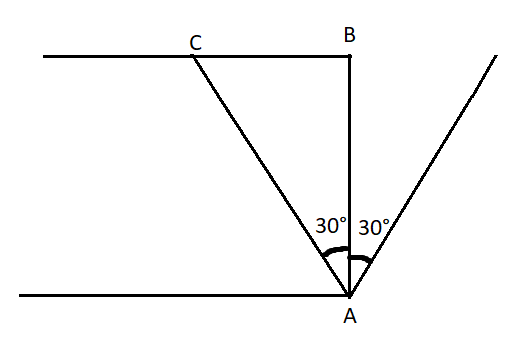
$\Delta ABC\tan {30^ \circ } = \dfrac{{BC}}{{AB}}$
$BC = 20mm\tan {30^ \circ }$
$l = N \times BC$
(A) $173$
(B) $84$
(C) $346$
(D) $42$

Answer 1

Hint The reflection of the mirror causes the deviation of the incident ray. Here we have two mirrors kept in parallel. For the incident ray falling at one end of one of the parallel mirrors will be deviated due to the reflection of the mirror. This will continue until it reaches the other end.

Step by step solution
The angle of incidence is given as ${30^ \circ }$
The separation between the mirrors is given as $20mm = 2cm$
By applying trigonometry,
The distance travelled by the ray to deviate from the normal in each reflection to reach the other end can be written as: $BC = 2 \times \tan {30^ \circ } = 1.1547cm$
Let us assume that the number of reflections is $N$
The total deviation that the incident ray underwent from the point of incidence can be written as: $1.1547N$
The length of the mirror is given by $2m = 200cm$
The length of the mirror is $l = N \times BC$
From this, we can write the number of reflections as,
$N = \dfrac{l}{{BC}}$
Substituting the values we get
$N = \dfrac{{200}}{{1.1547}} = 173.310$

The answer is Option (A): $173$

Note
As $0.310 \times 1.1547 = 0.3577 < 1.1547$ so it cannot be taken as one full reflection hence we can neglect the decimal part. The angle between the ray of incidence and the normal is called the angle of incidence. The angle between the ray of reflection and the normal is called the angle of reflection. The images produced by real objects in the plane mirrors are always virtual and the images produced by virtual objects are always real. Plane mirrors have an infinite focal length. The optical power of a plane will be zero. In plane mirrors the images will be laterally inverted.