Solveeit Logo
Login

Question

Question: Two parallel glass plates are dipped partly in the liquid of density 'd' keeping them vertical. If t...

Two parallel glass plates are dipped partly in the liquid of density 'd' keeping them vertical. If the distance between the plates is 'x', surface tension for liquids is T and angle of contact is θ\theta, then rise of liquid between the plates due to capillary will be

A

Tcos⁡θxd\frac { T \cos \theta } { x d }

B

2Tcos⁡θxdg\frac { 2 T \cos \theta } { x d g }

C

2Txdgcos⁡θ\frac { 2 T } { x d g \cos \theta }

D

Tcos⁡θxdg\frac { T \cos \theta } { x d g }

Answer

2Tcos⁡θxdg\frac { 2 T \cos \theta } { x d g }

Explanation

Solution

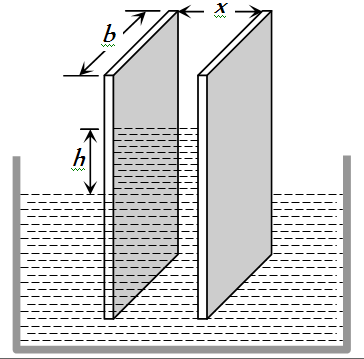
Let the width of each plate is b and due to surface tension liquid will rise upto height h then upward force due to surface tension

= 2Tbcos⁡θ2 T b \cos \theta …(i)

Weight of the liquid rises in between the plates

= Vdg=(bxh)dgV d g = ( b x h ) d g …(ii)

Equating (i) and (ii) we get , 2Tcos⁡θ=bxhdg2 T \cos \theta = b x h d g

∴h=2Tcos⁡θxdg\therefore h = \frac { 2 T \cos \theta } { x d g }