Question

Two parallel forces of magnitude 4 and 6 newton are acting on a body placed at 4m apart. Resultant will be-

Answer 1

The force acting on a body is equal to F=ma. Now, we will use each piece of information given to us, the direction of motion of the body remains unchanged. Hence the direction of force acting on the body remains the same as it was towards the initial direction of motion of the body. Then we can use mean force to find the resultant.

Complete step by step answer:
Magnitudes of two parallel forces given to us are 4N and 6N respectively.
For two parallel forces, if they are directed in the same direction then the resultant force is equal to 10N and if they are directed in opposite directions then the resultant force is equal to 2N.
In this case the resultant force can be calculated by calculating the position of force.
Resultant force = 4+6 = 10 N
To find the position of resultant force, let us take 4N as a reference point and draw a diagram.

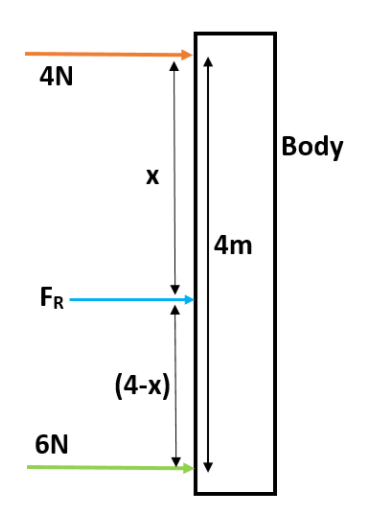
Now, the position of resultant force could be found by taking the mean as,
$\begin{aligned} & 4N\times x=6N\times (4-x) \\\ & \Rightarrow 4x=24-6x \\\ & \Rightarrow 10x=24 \\\ & \Rightarrow x=2.4m \\\ \end{aligned}$
So, we found that the resultant force 10N will be acting at 2.4m from the point where 4N force is applied.

Hence the answer is 10N at 2.4m from 4N force.

Note: Since, the direction of the force acting on the body doesn’t change, hence the angle between both the forces are zero. To understand it better, consider a football moving toward forward direction, a player sprints up to the ball and kicks it forward in the same direction. Now, if the player was to kick the ball in any other direction by kicking the ball at an angle using the same amount of force as in the previous case, then the magnitude of the force on the ball would remain the same, however the direction of the force and hence the direction of motion of the ball would change.