Question
Question: Two parallel chords of a circle whose diameter \[13cm\] are \[5cm\text{ }and\text{ }12cm\] . find th...
Two parallel chords of a circle whose diameter 13cm are 5cm and 12cm . find the distance between them if they lie on opposite of the centre and when they lie on the same side of centre.
Solution
First of all we will make the diagram of the given condition, to understand the condition very well. Then by using the properties of the circle and Pythagoras theorem to find out the length of the triangle.
Complete step by step answer:
Moving ahead with the question, we had a circle whose diameter is 13cm .
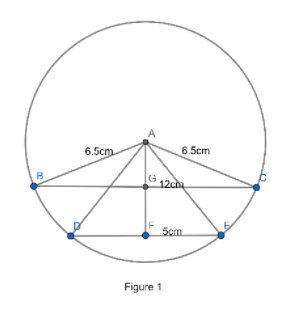
Let us first make the chords which are on the same side of centre as shown in figure 1. So according to the question we had to find out the distance between two chords i.e. between line segments marked as GF .
So let first find the AG and AF length using the triangle priority in ΔABG and ΔADF , and finally subtract AF and AG which will give us GF .
As by the circle property we know that whenever a line is dropped perpendicular to the chord from the centre of the circle then that line will cut the chord in two equal parts. So we can say that point G and F are the midpoint of chord BC and DE respectively.
So in the right angle triangle ΔAGB right angle at G , length of AB=6.5cm which is equal to radius of circle. And the length of BG=6cm as it is half of the chord length BC . So by applying Pythagoras theorem in ΔAGB we will get the unknown length AG , i.e.;
