Question
Question: Two parallel and opposite forces, each of magnitude 4000N, are applied tangentially to the upper and...
Two parallel and opposite forces, each of magnitude 4000N, are applied tangentially to the upper and lower faces of a cubical metal block of side 25cm. If the shear modulus for the metal is 8×1010Pa , then the displacement of the upper surface relative to the lower surface will be:
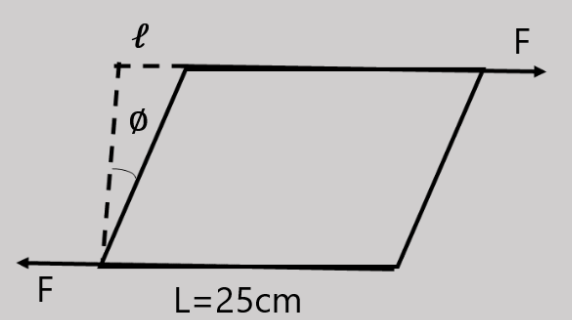
Solution
The strain caused by shear stress is called angle of deformation. The angle of shear strain (θ) is directly proportional to the shear force (F) applied on it and inversely proportional to the area (A) on which force applied and shear modulus (η) which is also called as modulus of rigidity.
Formula used: Angle of shear strain (θ) =AηF ;
Where,
F is applied force, A is the area on which force is applied and η is shear modulus or modulus of rigidity.
Complete step-by-step answer:
Let us first write the information given in the question.
Given,
F=4000N, Side=25cm=0.25m, η=8×1010Pa.
Let us find the area of the side on which the shear force is applied.
Area of the side can be find by using formula,
A=(side)2
A=(0.25)2
⇒0.0625m2
Now let us use the formula of angle of shear strain which is θ=AηF
Let us substitute the values in the formula, we get,
θ=0.0625×8×10104000
Let us further simplify it. On simplification we get,
θ=8×10−7
There is one more relation to angle of shear.
Angles of shear strain can also be defined as below.
θ=change in length/ original length
θ=lΔl
Let us substitute the values in this formula and obtain the change in length. We get,
Δl=θl=(8×10−7×0.25)m
Let us simplify the expression. On simplification we get,
Δl=2×10−7m
Hence, the required change in length is 2×10−7m.
Additional information: Shear force is the force applied perpendicular to the surface, for example, force applied when the paper is cut by scissors.
Shear stress is called the force which tends to deform the material example, stress applied on pipelines by flowing fluid through it.
Note: When an external force is applied tangentially on the surface of a body such that the opposite side of the body is kept fixed. Then the shape of the body changes while the volume remains unchanged. In this case, the body is said to be sheared.
For small strain, the ratio of shear stress and shear strain is known as modulus of rigidity (η) of the body.
